
【題目】下列四個命題中,正確的有__________.
①如果![]() 、
、![]() 與平面
與平面![]() 共面且
共面且![]() ,
,![]() ,那么
,那么![]() 就是平面
就是平面![]() 的一個法向量;
的一個法向量;
②設![]() :實數
:實數![]() ,
,![]() 滿足
滿足![]() ;
;![]() :實數
:實數![]() ,
,![]() 滿足
滿足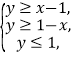 則
則![]() 是
是![]() 的充分不必要條件;
的充分不必要條件;
③已知橢圓![]() 與雙曲線
與雙曲線![]() 的焦點重合,
的焦點重合,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的離心率,則
的離心率,則![]() ,且
,且![]() ;
;
④菱形是圓的內接四邊形或是圓的外切四邊形.
科目:高中數學 來源: 題型:
【題目】觀察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
……
問:(1)此表第n行的第一個數與最后一個數分別是多少?
(2)此表第n行的各個數之和是多少?
(3)2012是第幾行的第幾個數?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() 當x∈[﹣
當x∈[﹣ ![]() ,
, ![]() ]時,恒有f(x+a)<f(x),則實數a的取值范圍是( )
]時,恒有f(x+a)<f(x),則實數a的取值范圍是( )
A.( ![]() ,
, ![]() )
)
B.(﹣1, ![]() )
)
C.( ![]() ,0)
,0)
D.( ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xoy中圓C的參數方程為 ![]() (α為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為
(α為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為 ![]() .
.
(1)求圓C的直角坐標方程及其圓心C的直角坐標;
(2)設直線l與曲線C交于A,B兩點,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=aex﹣xlnx,其中a∈R,e是自然對數的底數.
(Ⅰ)若f(x)是(0,+∞)上的增函數,求a的取值范圍;
(Ⅱ)若 ![]() ,證明:f(x)>0.
,證明:f(x)>0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對數列{an},如果k∈N*及λ1 , λ2 , …,λk∈R,使an+k=λ1an+k﹣1+λ2an+k﹣2+…+λkan成立,其中n∈N* , 則稱{an}為k階遞歸數列.給出下列三個結論: ①若{an}是等比數列,則{an}為1階遞歸數列;
②若{an}是等差數列,則{an}為2階遞歸數列;
③若數列{an}的通項公式為 ![]() ,則{an}為3階遞歸數列.
,則{an}為3階遞歸數列.
其中,正確結論的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com