
(本小題12分)已知三次函數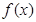 的導函數
的導函數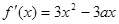 ,
,
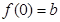 ,(
,(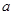 ,
,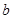
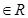 ).
).
(1)若曲線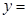
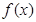 在點(
在點(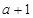 ,
,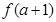 )處切線的斜率為12,求
)處切線的斜率為12,求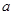 的值;
的值;
(2)若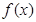 在區間[-1,1]上的最小值,最大值分別為-2和1,且
在區間[-1,1]上的最小值,最大值分別為-2和1,且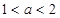 ,求函數
,求函數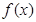 的解析式.
的解析式.
(1)a=3;(2)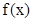 =
=
【解析】第一問中利用導數的幾何意義可得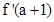 =12
=12
∴ 解得a的值
解得a的值
第二問∵ ,
,
∴ …5分
…5分
由 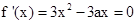 利用導數判定單調性得到。
利用導數判定單調性得到。
解:(1)由導數的幾何意義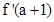 =12 ……………1分
=12 ……………1分
∴ ……………2分
……………2分
∴ 3a=9 ∴ a=3 ………………………3分
(2)∵ ,
,
∴ …5分
…5分
由 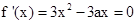 得
得 ,
,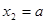
∵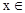 [-1,1],1<a<2
[-1,1],1<a<2
∴ 當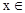 [-1,0)時,
[-1,0)時, ,
,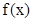 遞增;
遞增;
當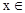 (0,1]時,
(0,1]時, ,
,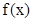 遞減。……………8分
遞減。……………8分
∴ 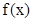 在區間[-1,1]上的最大值為f(0)
在區間[-1,1]上的最大值為f(0)
∵ 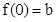 ,∴ b=1 ……………………10分
,∴ b=1 ……………………10分
∵ 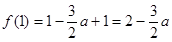 ,
,
∴ f(-1)<f(1) ∴
f(-1)是函數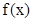 的最小值,
的最小值,
∴ -3/2 a=-2 ∴ a=4/3
∴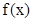 =
=


科目:高中數學 來源: 題型:
(本小題12分)已知![]() ,
,![]() ,直線
,直線![]() 與函數
與函數![]() 、
、![]() 的k*s#5^u圖象都相切,且與函數
的k*s#5^u圖象都相切,且與函數![]() 的k*s#5^u圖象的k*s#5^u切點的k*s#5^u橫坐標為
的k*s#5^u圖象的k*s#5^u切點的k*s#5^u橫坐標為![]() .
.
(Ⅰ)求直線![]() 的k*s#5^u方程及
的k*s#5^u方程及![]() 的k*s#5^u值;
的k*s#5^u值;
(Ⅱ)若![]() (其中
(其中![]() 是
是![]() 的k*s#5^u導函數),求函數
的k*s#5^u導函數),求函數![]() 的k*s#5^u最大值;
的k*s#5^u最大值;
(Ⅲ)當![]() 時,求證:
時,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源:2011年四川省瀘縣二中高2013屆春期重點班第一學月考試數學試題 題型:解答題
(本小題12分)已知等比數列 中,
中, 。
。
(1)求數列 的通項公式;
的通項公式;
(2)設等差數列 中,
中, ,求數列
,求數列 的前
的前 項和
項和 .
.
查看答案和解析>>
科目:高中數學 來源:2011云南省潞西市高二上學期期末考試數學試卷 題型:解答題
(本小題12分)
已知頂點在原點,焦點在 軸上的拋物線與直線
軸上的拋物線與直線 交于P、Q兩點,|PQ|=
交于P、Q兩點,|PQ|= ,求拋物線的方程
,求拋物線的方程
查看答案和解析>>
科目:高中數學 來源:2010年浙江省杭州市七校高二上學期期中考試數學文卷 題型:解答題
(本小題12分)
已知圓C: ;
;
(1)若直線 過
過 且與圓C相切,求直線
且與圓C相切,求直線 的方程.
的方程.
(2)是否存在斜率為1直線 ,使直線
,使直線 被圓C截得弦AB,以AB為直徑的圓經過原點O. 若存在,求
被圓C截得弦AB,以AB為直徑的圓經過原點O. 若存在,求
出直線 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2012屆山東省兗州市高二下學期期末考試數學(文) 題型:解答題
(本小題12分)已知函數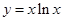
(1) 求這個函數的導數;
(2) 求這個函數的圖像在點 處的切線方程。
處的切線方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com