若1<x<3,a為何值時,x2-5x+3+a=0有兩解、一解、無解?
【答案】
分析:畫出方程x
2-5x+3=0對應函數y=-x
2+5x-3(1<x<3)的圖象,然后分析函數圖象與直線y=a的交點的情況,即可得到答案.
解答: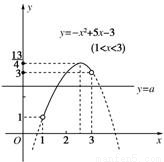
解:原方程化為:a=-x
2+5x-3,①,
作出函數y=-x
2+5x-3(1<x<3)的圖象如圖.
顯然該圖象與直線y=a的交點的橫坐標是方程①的解,
由圖可知:當3<a<
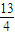
時,原方程有兩解;
當1<a≤3或a=
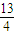
時,原方程有一解;
當a>
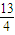
或a≤1時,原方程無解.
點評:本題考查的知識點是二次函數的性質,其中畫出函數y=-x
2+5x-3(1<x<3)的圖象,是解答本題的關鍵.
