
已知函數y=x+![]() 有如下性質:如果常數a>0,那么該函數在(0,
有如下性質:如果常數a>0,那么該函數在(0,![]() ]上為減函數,在[
]上為減函數,在[![]() ,+∞)上是增函數.
,+∞)上是增函數.
(1)如果函數y=x+![]() 在(0,4]上是減函數.在[4,+∞)上是增函數,求實常數b的值;
在(0,4]上是減函數.在[4,+∞)上是增函數,求實常數b的值;
(2)設常數c∈[1,4],求函數f(x)=x+![]() ,x∈[1,2]的最大值和最小值;
,x∈[1,2]的最大值和最小值;
(3)當n是正整數時,研究函數y(x)=xn+![]() (c>0)的單調性,并說明理由.
(c>0)的單調性,并說明理由.
|
解:(1)由函數y=x+ (2)∵c∈[1、4] ∴ 又∵f(x)=x+ 當 此時f(x)的最大值為f(2)=2+ 當c=2時f(2)-f(1)=0,f(2)=f(1). 此時f(x)的最大值為f(2)=f(1)=3. 當x∈(2,4]時,f(2)-f(1)<0,f(2)<f(1),此時f(x)的最大值為f(1)=1+c. (3)g′(x)=nxn-1- 令g′(x)=0,得x2n=c,∴x=± 又∵x≠0,列表分析,如下:
于是函數y(x)在(0, 當n是正奇數時,g(x)=xn+ 當n是正偶數時,g(x)=xn+ 思路分析:本題設計新穎,層層遞進,是演繹推理的典型應用.要正確理解題意根據已有的事實和正確的結論,按照嚴格的邏輯法進行證明,推理,尋找題目中的大前提和小前提. |


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源:湖北省武漢市武昌區2012屆高三5月調研考試數學文科試題 題型:013
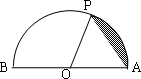
已知點P在半徑為1的半圓周上沿著A→P→B路徑運動,設弧![]() 的長度為x,弓形面積為f(x)(如圖所示的陰影部分),則關于函數y=f(x)的有如下結論:
的長度為x,弓形面積為f(x)(如圖所示的陰影部分),則關于函數y=f(x)的有如下結論:
①函數y=f(x)的定義域和值域都是[0,π];
②如果函數y=f(x)的定義域R,則函數y=f(x)是周期函數;
③如果函數y=f(x)的定義域R,則函數y=f(x)是奇函數;
④函數y=f(x)在區間[0,π]上是單調遞增函數.
以上結論的正確個數是
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com