
【題目】已知函數fn(x)=a1x+a2x2+a3x3+…+anxn , 且fn(﹣1)=(﹣1)nn,n∈N* , 設函數g(n)=  ,若bn=g(2n+4),n∈N* , 則數列{bn}的前n(n≥2)項和Sn等于 .
,若bn=g(2n+4),n∈N* , 則數列{bn}的前n(n≥2)項和Sn等于 .
【答案】2n+n﹣1
【解析】解:由函數g(n)= 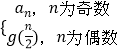 , 可得bn=g(2n+4)=g(2n﹣1+2)=g(2n﹣2+1)=a
, 可得bn=g(2n+4)=g(2n﹣1+2)=g(2n﹣2+1)=a ![]() ,
,
由函數fn(x)=a1x+a2x2+a3x3+…+anxn , 且fn(﹣1)=(﹣1)nn,
可得﹣a1+a2﹣a3+…+an(﹣1)n=(﹣1)nn,①
n=1時,﹣a1=﹣1,可得a1=1;
n≥2時,﹣a1+a2﹣a3+…+an﹣1(﹣1)n﹣1=(﹣1)n﹣1(n﹣1),②
①﹣②可得an(﹣1)n=(﹣1)nn﹣(﹣1)n﹣1(n﹣1),
化簡可得an=2n﹣1,對n=1也成立.
則bn=a ![]() =2n﹣1+1,
=2n﹣1+1,
則數列{bn}的前n(n≥2)項和Sn等于(1+2+4+…+2n﹣1)+n
= ![]() +n=2n+n﹣1.
+n=2n+n﹣1.
故答案為:2n+n﹣1.
由分段函數,求得bn=a ![]() ,再由函數fn(x),求得n=1時,a1=1,將n換為n﹣1,作差可得an=2n﹣1,進而得到
,再由函數fn(x),求得n=1時,a1=1,將n換為n﹣1,作差可得an=2n﹣1,進而得到
bn=2n﹣1+1,再由數列的求和方法:分組求和,結合等比數列的求和公式,計算即可得到所求和.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某電視臺推出一檔游戲類綜藝節目,選手面對1﹣5號五扇大門,依次按響門上的門鈴,門鈴會播放一段音樂,選手需正確回答這首歌的名字,回答正確,大門打開,并獲得相應的家庭夢想基金,回答每一扇門后,選手可自由選擇帶著目前的獎金離開,還是繼續挑戰后面的門以獲得更多的夢想基金,但是一旦回答錯誤,游戲結束并將之前獲得的所有夢想基金清零;整個游戲過程中,選手有一次求助機會,選手可以詢問親友團成員以獲得正確答案. 1﹣5號門對應的家庭夢想基金依次為3000元、6000元、8000元、12000元、24000元(以上基金金額為打開大門后的累積金額,如第三扇大門打開,選手可獲基金總金額為8000元);設某選手正確回答每一扇門的歌曲名字的概率為pi(i=1,2,…,5),且pi= ![]() (i=1,2,…,5),親友團正確回答每一扇門的歌曲名字的概率均為
(i=1,2,…,5),親友團正確回答每一扇門的歌曲名字的概率均為 ![]() ,該選手正確回答每一扇門的歌名后選擇繼續挑戰后面的門的概率均為
,該選手正確回答每一扇門的歌名后選擇繼續挑戰后面的門的概率均為 ![]() ;
;
(1)求選手在第三扇門使用求助且最終獲得12000元家庭夢想基金的概率;
(2)若選手在整個游戲過程中不使用求助,且獲得的家庭夢想基金數額為X(元),求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣alnx,g(x)=﹣ ![]() ,其中a∈R
,其中a∈R
(1)設函數h(x)=f(x)﹣g(x),求函數h(x)的單調區間;
(2)若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A.?x0∈R,sinx0+cosx0= ![]()
B.?x≥0且x∈R,2x>x2
C.已知a,b為實數,則a>2,b>2是ab>4的充分條件
D.已知a,b為實數,則a+b=0的充要條件是 ![]() =﹣1
=﹣1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x),當x∈[0,2]時,f(x)=4(1﹣|x﹣1|),且對于任意實數x∈[2n﹣2,2n+1﹣2](n∈N* , n≥2),都有f(x)= ![]() f(
f( ![]() ﹣1).若g(x)=f(x)﹣logax有且只有三個零點,則a的取值范圍是( )
﹣1).若g(x)=f(x)﹣logax有且只有三個零點,則a的取值范圍是( )
A.[2,10]
B.[ ![]() ,
, ![]() ]
]
C.(2,10)
D.[2,10)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓C: ![]() +
+ ![]() =1(a>b>0)的左、右焦點分別為F1、F2 , 上頂點為A,過A與AF2垂直的直線交x軸負半軸于Q點,且F1恰好是線段QF2的中點.
=1(a>b>0)的左、右焦點分別為F1、F2 , 上頂點為A,過A與AF2垂直的直線交x軸負半軸于Q點,且F1恰好是線段QF2的中點.
(1)若過A、Q、F2三點的圓恰好與直線3x﹣4y﹣7=0相切,求橢圓C的方程;
(2)在(1)的條件下,B是橢圓C的左頂點,過點R( ![]() ,0)作與x軸不重合的直線l交橢圓C于E、F兩點,直線BE、BF分別交直線x=
,0)作與x軸不重合的直線l交橢圓C于E、F兩點,直線BE、BF分別交直線x= ![]() 于M、N兩點,若直線MR、NR的斜率分別為k1 , k2 , 試問:k1k2是否為定值?若是,求出該定值;若不是,請說明理由.
于M、N兩點,若直線MR、NR的斜率分別為k1 , k2 , 試問:k1k2是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖在直角梯形BB1C1C中,∠CC1B1=90°,BB1∥CC1 , CC1=B1C1=2BB1=2,D是CC1的中點.四邊形AA1C1C可以通過直角梯形BB1C1C以CC1為軸旋轉得到,且二面角B1﹣CC1﹣A為120°. 
(1)若點E是線段A1B1上的動點,求證:DE∥平面ABC;
(2)求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com