
【題目】已知a是實常數,函數![]() .
.
(1)若曲線![]() 在
在![]() 處的切線過點A(0,﹣2),求實數a的值;
處的切線過點A(0,﹣2),求實數a的值;
(2)若![]() 有兩個極值點
有兩個極值點![]() (
(![]() ),
),
①求證:![]() ;
;
②求證:![]() .
.
【答案】(1)證明詳見解析;(2)證明詳見解析.
【解析】
試題本題考查導數的運用:求切線方程和單調區間、極值,主要考查導數的幾何意義和分類討論的思想方法,注意函數的單調性的運用,屬于中檔題.第一問,求出![]() 的導數,求得切線的斜率和切點,由點斜式方程可得切線方程,代入點(0,﹣2),即可解得a;第二問,①依題意:
的導數,求得切線的斜率和切點,由點斜式方程可得切線方程,代入點(0,﹣2),即可解得a;第二問,①依題意:![]() 有兩個不等實根
有兩個不等實根![]() (
(![]() ),設
),設![]() ,求出導數,討論當a≥0時,當a<0時,求得函數g(x)的單調性,令極大值大于0,解不等式即可得證;②由①知:
,求出導數,討論當a≥0時,當a<0時,求得函數g(x)的單調性,令極大值大于0,解不等式即可得證;②由①知:![]() ,
,![]() 變化,求得
變化,求得![]() 的增區間,通過導數,判斷
的增區間,通過導數,判斷![]() ,設
,設![]() (0<x<1),求得h(x)的單調性,即可得證.
(0<x<1),求得h(x)的單調性,即可得證.
試題解析:(1)由已知可得,![]() (x>0),切點
(x>0),切點![]() ,
,
![]() 在x=1處的切線斜率為
在x=1處的切線斜率為![]() ,
,
切線方程:![]() ,
,
把![]() 代入得:a=1;
代入得:a=1;
(2)證明:①依題意:![]() 有兩個不等實根
有兩個不等實根![]() (
(![]() ),
),
設![]() 則:
則:![]() (x>0)
(x>0)
當a≥0時,有![]() ,所以
,所以![]() 是增函數,不符合題意;
是增函數,不符合題意;
當a<0時:由![]() 得:
得:![]() ,
,
列表如下:

依題意:![]() ,解得:
,解得:![]() ,
,
綜上可得,![]() 得證;
得證;
②由①知:![]() ,
,![]() 變化如下:
變化如下:
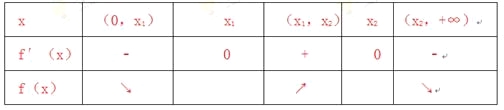
由表可知:![]() 在[x1,x2]上為增函數,所以:
在[x1,x2]上為增函數,所以:![]()
又![]() ,故
,故![]() ,
,
由(1)知:![]() ,
,![]() (
(![]() )
)
設![]() (
(![]() ),則
),則![]() 成立,所以
成立,所以![]() 單調遞減,
單調遞減,
故:![]() ,也就是
,也就是![]() ,
,
綜上所證:![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】某新建小區規劃利用一塊空地進行配套綠化.已知空地的一邊是直路![]() ,余下的外圍是拋物線的一段弧,直路
,余下的外圍是拋物線的一段弧,直路![]() 的中垂線恰是該拋物線的對稱軸(如圖),點O是
的中垂線恰是該拋物線的對稱軸(如圖),點O是![]() 的中點.擬在這個地上劃出一個等腰梯形
的中點.擬在這個地上劃出一個等腰梯形![]() 區域種植草坪,其中
區域種植草坪,其中![]() 均在該拋物線上.經測量,直路
均在該拋物線上.經測量,直路![]() 長為60米,拋物線的頂點P到直路
長為60米,拋物線的頂點P到直路![]() 的距離為60米.設點C到拋物線的對稱軸的距離為m米,到直路
的距離為60米.設點C到拋物線的對稱軸的距離為m米,到直路![]() 的距離為n米.
的距離為n米.

(1)求出n關于m的函數關系式.
(2)當m為多大時,等腰梯形草坪![]() 的面積最大?并求出其最大值.
的面積最大?并求出其最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知半徑為
中,已知半徑為![]() 的圓
的圓![]() ,圓心在
,圓心在![]() 軸正半軸上,且與直線
軸正半軸上,且與直線![]() 相切.
相切.
(1)求圓![]() 的方程;
的方程;
(2)在圓![]() 上,是否存在點
上,是否存在點![]() ,滿足
,滿足![]() ,其中,點
,其中,點![]() 的坐標是
的坐標是![]() .若存在,指出有幾個這樣的點;若不存在,請說明理由;
.若存在,指出有幾個這樣的點;若不存在,請說明理由;
(3)若在圓![]() 上存在點
上存在點![]() ,使得直線
,使得直線![]() 與圓
與圓![]() 相交不同兩點
相交不同兩點![]() ,求
,求![]() 的取值范圍.并求出使得
的取值范圍.并求出使得![]() 的面積最大的點
的面積最大的點![]() 的坐標及對應的
的坐標及對應的![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD的底面ABCD為直角梯形,AD//BC,且![]() ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E為AD的中點,△PAD為等邊三角形,M是棱PC上的一點,設
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E為AD的中點,△PAD為等邊三角形,M是棱PC上的一點,設![]() (M與C不重合).
(M與C不重合).
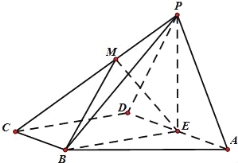
(1)求證:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角為150°,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的標準方程為
的標準方程為![]() ,該橢圓經過點
,該橢圓經過點![]() ,且離心率為
,且離心率為![]() .
.
(1)求橢圓的標準方程;
(2)過橢圓![]() 長軸上一點
長軸上一點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() .若弦
.若弦![]() 的中點分別為
的中點分別為![]() ,證明:直線
,證明:直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題![]() 方程
方程![]() 表示雙曲線;命題
表示雙曲線;命題![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 為假,
為假, ![]() 為真,求
為真,求![]() 的取值范圍.
的取值范圍.
【答案】![]()
【解析】試題分析:由命題![]() 方程
方程![]() 表示雙曲線,求出
表示雙曲線,求出![]() 的取值范圍,由命題
的取值范圍,由命題![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范圍,由
的取值范圍,由![]() 為假,
為假, ![]() 為真,得出
為真,得出![]() 一真一假,分兩種情況即可得出
一真一假,分兩種情況即可得出![]() 的取值范圍.
的取值范圍.
試題解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范圍為
范圍為![]()
【題型】解答題
【結束】
18
【題目】如圖,設![]() 是圓
是圓![]() 上的動點,點
上的動點,點![]() 是
是![]() 在
在![]() 軸上的投影,
軸上的投影, ![]() 為
為![]() 上一點,且
上一點,且![]() .
.

(1)當![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)求過點![]() 且斜率為
且斜率為![]() 的直線被
的直線被![]() 所截線段的長度.
所截線段的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com