
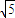 ,CD⊥⊙O所在的平面,BE∥CD,CD=4,BC=2,且BE=1,
,CD⊥⊙O所在的平面,BE∥CD,CD=4,BC=2,且BE=1,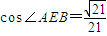 .
. ?若存在,確定點M的位置,若不存在,請說明理由.
?若存在,確定點M的位置,若不存在,請說明理由.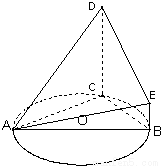
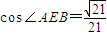 ,易得AB是⊙O的直徑,則AC⊥BC由線面垂直的判定定理可得CD⊥平面ABC,再由面面垂直的判定定理可得平面ADC⊥平面BCDE;
,易得AB是⊙O的直徑,則AC⊥BC由線面垂直的判定定理可得CD⊥平面ABC,再由面面垂直的判定定理可得平面ADC⊥平面BCDE; ,我們可以構造關于x的方程,解方程即可求出x值,進而得到點M的位置.
,我們可以構造關于x的方程,解方程即可求出x值,進而得到點M的位置. ,根據向量夾角公式,我們可以構造關于λ的方程,解方程即可得到λ值,進而得到點M的位置.
,根據向量夾角公式,我們可以構造關于λ的方程,解方程即可得到λ值,進而得到點M的位置.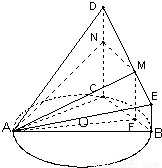 解:(1)∵CD⊥平面ABC,BE∥CD
解:(1)∵CD⊥平面ABC,BE∥CD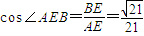
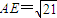 ,
,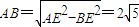 …(2分)
…(2分)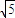 ,
,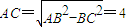 ,…(6分)
,…(6分)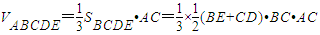 =
=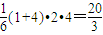 …(9分)
…(9分)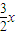 ,MF=
,MF=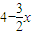 …(11分)
…(11分)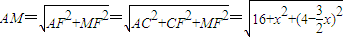
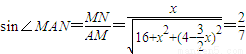 …(12分)
…(12分)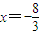 (舍去)
(舍去)  ,…(13分)
,…(13分)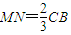 ,從而滿足條件的點M存在,且
,從而滿足條件的點M存在,且 …(14分)
…(14分)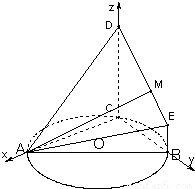 :
: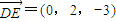 …(10分)
…(10分)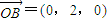 ,
,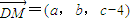 ,
,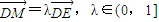 ∴
∴ ,
,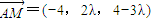
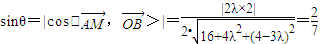 …(12分)
…(12分)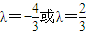 ,…(13分)
,…(13分)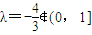 應舍去,而
應舍去,而
 …(14分)
…(14分) ,構造滿足條件的方程.
,構造滿足條件的方程. 

 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:
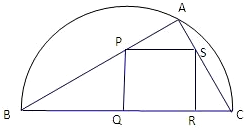 如圖,某小區準備綠化一塊直徑為BC的半圓形空地,△ABC外的地方種草,△ABC的內接正方形PQRS為一水池,其余地方種花.若BC=20米,∠ABC=θ,設△ABC的面積為S1,正方形PQRS的面積為S2,將比值
如圖,某小區準備綠化一塊直徑為BC的半圓形空地,△ABC外的地方種草,△ABC的內接正方形PQRS為一水池,其余地方種花.若BC=20米,∠ABC=θ,設△ABC的面積為S1,正方形PQRS的面積為S2,將比值| S1 | S2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
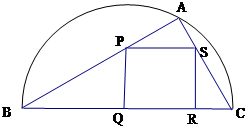 如圖,某小區準備綠化一塊直徑為BC的半圓形空地,△ABC的內接正方形PQRS為一水池,△ABC外的地方種草,其余地方種花.若BC=a,∠ABC=θ,設△ABC的面積為S1,正方形PQRS的面積為S2,將比值
如圖,某小區準備綠化一塊直徑為BC的半圓形空地,△ABC的內接正方形PQRS為一水池,△ABC外的地方種草,其余地方種花.若BC=a,∠ABC=θ,設△ABC的面積為S1,正方形PQRS的面積為S2,將比值| S1 | S2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
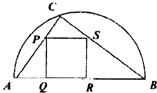 如圖,某小區準備綠化一塊直徑為AB的半圓形空地,點C在半圓弧上,半圓內△ABC外的地方種草,△ABC的內接正方形PQRS內部為一水池,其余地方種花,若AB=2a,∠CAB=θ,設△ABC的面積為S1,正方形PQRS的邊長為x,面積為S2,將比值
如圖,某小區準備綠化一塊直徑為AB的半圓形空地,點C在半圓弧上,半圓內△ABC外的地方種草,△ABC的內接正方形PQRS內部為一水池,其余地方種花,若AB=2a,∠CAB=θ,設△ABC的面積為S1,正方形PQRS的邊長為x,面積為S2,將比值| S1 |
| S2 |
| 2asin2θ |
| 2+sin2θ |
查看答案和解析>>
科目:高中數學 來源: 題型:
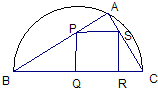 (2007•楊浦區二模)如圖,某小區準備綠化一塊直徑為BC的半圓形空地,△ABC外的地方種草,△ABC的內接正方形PQRS為一水池,其余地方種花.若BC=a,∠ABC=θ,設△ABC的面積為S1,正方形PQRS的面積為S2,將比值
(2007•楊浦區二模)如圖,某小區準備綠化一塊直徑為BC的半圓形空地,△ABC外的地方種草,△ABC的內接正方形PQRS為一水池,其余地方種花.若BC=a,∠ABC=θ,設△ABC的面積為S1,正方形PQRS的面積為S2,將比值| S1 | S2 |
查看答案和解析>>
科目:高中數學 來源:2007年上海市楊浦區、靜安區高考數學二模試卷(文理合卷)(解析版) 題型:解答題
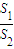 稱為“規劃合理度”.
稱為“規劃合理度”.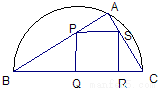
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com