【答案】
分析:(1)由題意,由于告訴了橢圓為焦點(diǎn)在x軸的橢圓所以可以利用定義設(shè)出 方程,然后建立a,b的方程求解即可;
(2)問是否存在的問題在圓錐曲線中就先假設(shè)存在,分斜率存在于不存在加以討論,并把直線方程與橢圓方程進(jìn)行連聯(lián)立,利用設(shè)而不求整體代換進(jìn)行求解.
解答:解:(Ⅰ)設(shè)橢圓C的方程為:

+

=1(a>b>0),則a
2-b
2=1.①
∵當(dāng)l垂直于x軸時(shí),A,B兩點(diǎn)坐標(biāo)分別是(1,

)和(1,-

),
∴

•

=(1,

)•(1,-

)=1-

,則1-

=

,即a
2=6b
4.②
由①,②消去a,得6b
4-b
2-1=0.∴b
2=

或b
2=-

.
當(dāng)b
2=

時(shí),a
2=

.因此,橢圓C的方程為

+2y
2=1.
(Ⅱ)設(shè)存在滿足條件的直線l.
(1)當(dāng)直線l垂直于x軸時(shí),由(Ⅰ)的解答可知|AB|=

=

,焦點(diǎn)F到右準(zhǔn)線的距離為d=

-c=

,
此時(shí)不滿足d=

|AB|.
因此,當(dāng)直線l垂直于x軸時(shí)不滿足條件.
(2)當(dāng)直線l不垂直于x軸時(shí),設(shè)直線l的斜率為k,則直線l的方程為y=k(x-1).
由

⇒(6k
2+2)x
2-12k
2x+6k
2-3=0,
設(shè)A,B兩點(diǎn)的坐標(biāo)分別為(x
1,y
1)和(x
2,y
2),則x
1+x
2=

,x
1x
2=

.
|AB|=

|x
1-x
2|=

=

=-

.
又設(shè)AB的中點(diǎn)為M,則x
M=

=

.
當(dāng)△ABP為正三角形時(shí),直線MP的斜率為k
MP=-

.
∵x
p=

,∴|MP|=

|x
p-x
M|=

•(

-

)=

•

.
當(dāng)△ABP為正三角形時(shí),|MP|=

|AB|,即

•

=

•

,
解得k
2=1,k=±1.
因此,滿足條件的直線l存在,且直線l的方程為x-y-1=0或x+y-1=0.
點(diǎn)評:(1)次問重點(diǎn)考查了利用方程的思想由題意列出變量a,b的兩個(gè)方程,然后求解曲線的軌跡方程;
(2)次問重點(diǎn)考查了分類討論的思想及把直線方程與圓錐曲線方程進(jìn)行聯(lián)立設(shè)而不求整體代換的思想,還有對于圓錐曲線中是否存在利用假設(shè)的解題方法.

 .
. +
+ =1(a>b>0),則a2-b2=1.①
=1(a>b>0),則a2-b2=1.① )和(1,-
)和(1,- ),
), •
• =(1,
=(1, )•(1,-
)•(1,- )=1-
)=1- ,則1-
,則1- =
= ,即a2=6b4.②
,即a2=6b4.② 或b2=-
或b2=- .
. 時(shí),a2=
時(shí),a2= .因此,橢圓C的方程為
.因此,橢圓C的方程為 +2y2=1.
+2y2=1. =
= ,焦點(diǎn)F到右準(zhǔn)線的距離為d=
,焦點(diǎn)F到右準(zhǔn)線的距離為d= -c=
-c= ,
, |AB|.
|AB|. ⇒(6k2+2)x2-12k2x+6k2-3=0,
⇒(6k2+2)x2-12k2x+6k2-3=0, ,x1x2=
,x1x2= .
. |x1-x2|=
|x1-x2|= =
= =-
=- .
. =
= .
. .
. ,∴|MP|=
,∴|MP|= |xp-xM|=
|xp-xM|= •(
•( -
- )=
)= •
• .
. |AB|,即
|AB|,即 •
• =
= •
• ,
,


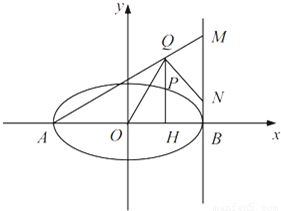
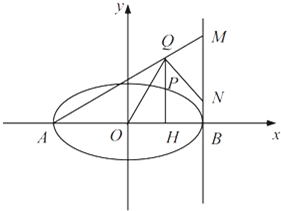 (2013•深圳一模)已知橢圓C 的中心為原點(diǎn)O,焦點(diǎn)在x 軸上,離心率為
(2013•深圳一模)已知橢圓C 的中心為原點(diǎn)O,焦點(diǎn)在x 軸上,離心率為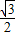 ,且點(diǎn)
,且點(diǎn)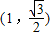 在該橢圓上.
在該橢圓上.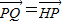 ,直線AQ與過點(diǎn)B 且垂直于x 軸的直線交于點(diǎn)M,
,直線AQ與過點(diǎn)B 且垂直于x 軸的直線交于點(diǎn)M,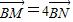 .求證:∠OQN為銳角.
.求證:∠OQN為銳角.