
分析 (Ⅰ)利用三角函數恒等變換的應用化簡函數解析式可得f(x)=sin(2x+$\frac{π}{3}$)-$\frac{\sqrt{3}}{2}$,利用周期公式即可計算得解.
(Ⅱ)由已知可求范圍2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],利用正弦函數的圖象和性質即可求得最小值.
解答 (本題滿分為12分)
解:(Ⅰ)由題意得f(x)=cosxsinx-$\sqrt{3}$sin2x
=$\frac{1}{2}$sin2x-$\sqrt{3}$($\frac{1-cos2x}{2}$)
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x-$\frac{\sqrt{3}}{2}$
=sin(2x+$\frac{π}{3}$)-$\frac{\sqrt{3}}{2}$ …(5分)
∴T=$\frac{2π}{2}=π$.…(6分)
(Ⅱ)∵x∈[0,$\frac{π}{4}$],∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],
∴f(x)的最小值為f($\frac{5π}{6}$)=$\frac{1-\sqrt{3}}{2}$.…(12分)
點評 本題主要考查了三角函數恒等變換的應用,周期公式,正弦函數的圖象和性質的應用,考查了轉化思想和數形結合思想的應用,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 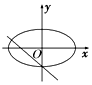 | B. | 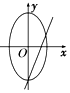 | C. | 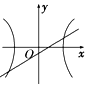 | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{3}$ | B. | $\sqrt{10}$ | C. | $\sqrt{14}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com