
【題目】設數列{an}滿足:a1=1,an+1=3an , n∈N* . 設Sn為數列{bn}的前n項和,已知b1≠0,2bn﹣b1=S1Sn , n∈N*(Ⅰ)求數列{an},{bn}的通項公式;
(Ⅱ)設cn=bnlog3an , 求數列{cn}的前n項和Tn .
【答案】解:(Ⅰ)∵an+1=3an , ∴{an}是公比為3,首項a1=1的等比數列, ∴通項公式為an=3n﹣1 .
∵2bn﹣b1=S1Sn , ∴當n=1時,2b1﹣b1=S1S1 ,
∵S1=b1 , b1≠0,∴b1=1.
∴當n>1時,bn=Sn﹣Sn﹣1=2bn﹣2bn﹣1 , ∴bn=2bn﹣1 ,
∴{bn}是公比為2,首項a1=1的等比數列,
∴通項公式為bn=2n﹣1 .
(Ⅱ)cn=bnlog3an=2n﹣1log33n﹣1=(n﹣1)2n﹣1 ,
Tn=020+121+222+…+(n﹣2)2n﹣2+(n﹣1)2n﹣1…①
2Tn=021+122+223+…+(n﹣2)2n﹣1+(n﹣1)2n…②
①﹣②得:﹣Tn=020+21+22+23+…+2n﹣1﹣(n﹣1)2n
=2n﹣2﹣(n﹣1)2n=﹣2﹣(n﹣2)2n
∴Tn=(n﹣2)2n+2.
【解析】(Ⅰ)判斷an}是等比數列,求出通項公式,判斷{bn}是等比數列,求出通項公式為bn . (Ⅱ)化簡cn的表達式,利用錯位相減法求解Tn即可.
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識,掌握數列{an}的前n項和sn與通項an的關系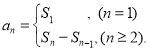 .
.


科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 是一幢6層的寫字樓,每層高均為3m,在
是一幢6層的寫字樓,每層高均為3m,在![]() 正前方36m處有一建筑物
正前方36m處有一建筑物![]() ,從樓頂
,從樓頂![]() 處測得建筑物
處測得建筑物![]() 的張角為
的張角為![]() .
.
(1)求建筑物![]() 的高度;
的高度;
(2)一攝影愛好者欲在寫字樓![]() 的某層拍攝建筑物
的某層拍攝建筑物![]() .已知從攝影位置看景物所成張角最大時,拍攝效果最佳.問:該攝影愛好者在第幾層拍攝可取得最佳效果(不計人的高度)?
.已知從攝影位置看景物所成張角最大時,拍攝效果最佳.問:該攝影愛好者在第幾層拍攝可取得最佳效果(不計人的高度)?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+b(a>0,a≠1)滿足f(x+y)=f(x)f(y),且f(3)=8.
(1)求實數a,b的值;
(2)若不等式|x﹣1|<m的解集為(b,a),求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中正確的個數是 ( )
①“x=![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
②若a>b,則am2>bm2;
③命題“x∈R,sinx≤1”的否定是“x∈R,sinx>1”;
④函數f(x)=![]() -cosx在[0,+∞)內有且僅有兩個零點.
-cosx在[0,+∞)內有且僅有兩個零點.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某種產品的年固定成本為250萬元,每生產![]() 千件,需另投入成本為
千件,需另投入成本為![]() 萬元,當年產量不足80千件時,
萬元,當年產量不足80千件時, ![]() (萬元);當年產量不少于80千件時,
(萬元);當年產量不少于80千件時, ![]() (萬元).通過市場分析,若每件售價為500元時,該廠年內生產的商品能全部銷售完.
(萬元).通過市場分析,若每件售價為500元時,該廠年內生產的商品能全部銷售完.
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】長春市的“名師云課”活動自開展以來獲得廣大家長和學生的高度贊譽,在我市推出的第二季名師云課中,數學學科共計推出36節云課,為了更好地將課程內容呈現給學生,現對某一時段云課的點擊量進行統計:
點擊量 |
|
|
|
節數 | 6 | 18 | 12 |
(Ⅰ)現從36節云課中采用分層抽樣的方式選出6節,求選出的點擊量超過3000的節數.
(Ⅱ)為了更好地搭建云課平臺,現將云課進行剪輯,若點擊量在區間![]() 內,則需要花費40分鐘進行剪輯,若點擊量在區間
內,則需要花費40分鐘進行剪輯,若點擊量在區間![]() 內,則需要花費20分鐘進行剪輯,點擊量超過3000,則不需要剪輯,現從(Ⅰ)中選出的6節課中隨機取出2節課進行剪輯,求剪輯時間
內,則需要花費20分鐘進行剪輯,點擊量超過3000,則不需要剪輯,現從(Ⅰ)中選出的6節課中隨機取出2節課進行剪輯,求剪輯時間![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在公比為正數的等比數列{an}中, ![]() ,
, ![]() ,數列{bn}(bn>0)的前n項和為Sn滿足
,數列{bn}(bn>0)的前n項和為Sn滿足 ![]() (n≥2),且S10=100.
(n≥2),且S10=100.
( I)求數列{an}和數列{bn}的通項公式;
( II)求數列{anbn}的前n項和為Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上的點到二定點
上的點到二定點![]() 、
、![]()
![]() 的距離之和為定值
的距離之和為定值![]() ,以
,以![]() 為圓心半徑為4的圓
為圓心半徑為4的圓![]() 與
與![]() 有兩交點,其中一交點為
有兩交點,其中一交點為![]() ,
, ![]() 在y軸正半軸上,圓
在y軸正半軸上,圓![]() 與x軸從左至右交于
與x軸從左至右交于![]() 二點,
二點, ![]() .
.
(1)求曲線![]() 、
、![]() 的方程;
的方程;
(2)曲線![]() ,直線
,直線![]() 與
與![]() 交于點
交于點![]() ,過
,過![]() 點的直線
點的直線![]() 與曲線
與曲線![]() 交于
交于![]() 二點,過
二點,過![]() 做
做![]() 的切線
的切線![]() ,
, ![]() 交于
交于![]() .當
.當![]() 在x軸上方時,是否存在點
在x軸上方時,是否存在點![]() ,滿足
,滿足![]() ,并說明理由.
,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com