
已知f(x)=px2-q,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范圍.
|
解:依題意,有 ∴ ∴f(3)=9p-q= ∵-1≤f(2)≤5,∴- -4≤f(1)≤-1,∴ ∴- 即-1≤f(3)≤20. 當 當 分析:可考慮將f(3)寫成f(1)、f(2)的線性組合,即f(3)=mf(1)+nf(2)的形式,然后用不等式的運算性質推算f(3)的取值范圍. |
|
注:這種類型的題目常見的錯誤是 由 1≤q≤7,從而-7≤f(3)=9p-q≤26. 事實上,f(3)不可能取得[-7,26]上的一切值,p、q是兩個相互聯系、相互制約的量,在得出0≤p≤3,1≤q≤7后,并不意味著p、q可以獨立地取得區間[0,3]及[1,7]上的一切值.如取p=0,q=7時,p-q=-7,已不滿足-4≤p-q≤-1. 所以用不等式的運算性質求范圍時,盡量只用一次,如果需要多次使用性質時,要考慮等號能否取到,否則可能會出現范圍過大或過小的情況. |


科目:高中數學 來源:學習周報 數學 北師大課標高二版(必修5) 2009-2010學年 第10期 總第166期 北師大課標版(必修5) 題型:022
已知
f(x)=px2-q,且-4≤f(1)≤-1,-1≤f(2)≤5,則f(3)的取值范圍為________.查看答案和解析>>
科目:高中數學 來源:設計選修數學-2-2蘇教版 蘇教版 題型:013
已知函數f(x)=x3-px2-qx的圖象與x軸切于(1,0)點,則f(x)的極值為
極大值為![]() ,極小值為0
,極小值為0
極大值為0,極小值為![]()
極小值為![]() ,極大值為0
,極大值為0
極小值為0,極大值為![]()
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖北岳中高中一輪復習理科數學滾動測試三解析版 題型:選擇題
已知函數f(x)=x3-px2-qx的圖象與x軸切于(1,0)點,則f(x)的極大值、極小值分別為( )
A. 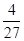 ,0
B.0,
,0
B.0,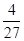 C.-
C.-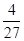 ,0 D.0,-
,0 D.0,-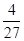
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com