①③⑤
分析:由輔助角公式,化簡得f(x)=

sin(2x+θ),結合已知不等式得f(

)是函數的最大或最小值,從而得到
f(x)=

sin(2x+

+kπ)=±

sin(2x+

).再根據三角函數y=Asin(ωx+φ)的圖象與性質,對各選項逐個加以判斷,可得①③⑤通過證明可得其正確性,而②④存在反例說明它們不正確.
解答:f(x)=asin2x+bcos2x=

sin(2x+θ),其中角θ滿足cosθ=
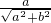
,sinθ=
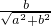
∵f(x)≤|f(

)|對一切x∈R恒成立,
∴f(

)=

或-

,得2×

+θ=

+kπ,k∈Z
因此θ=

+kπ,k∈Z.f(x)=

sin(2x+

+kπ)=

sin(2x+

)或-

sin(2x+

)
對于①,因為sin(2×

+

)=sin2π=0,所以f(

)=±

sin(2×

+

)=0,故①正確;
對于②,|f(

)|=|

sin(2×

+

)|=


∵|f(

)|=|

sin(2×

+

)|=

sin
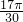
<


∴|f(

)|>|f(

)|,故②不正確;
對于③,根據函數的表達式,得f(-x)≠±f(x),故y=f(x)既不是奇函數也不是偶函數,故③正確;
對于④,因為函數的表達式f(x)=

sin(2x+

)或-

sin(2x+

),
表達式不確定,故[kπ+

,kπ+

](k∈Z)不一定是增區間,故④不正確;
對于⑤,采用反證法
設經過點(a,b)的一條直線與函數y=f(x)的圖象不相交,則此直線與x軸平行
方程為y=b,且|b|>

,平方得b
2>a
2+b
2矛盾,故假設不成立
∴經過點(a,b)的所有直線均與函數y=f(x)的圖象相交.故⑤正確.
故答案為:①③⑤
點評:本題給出符合已知條件的三角函數表達式,叫我們判斷幾個選項的正確性,著重考查了函數y=Asin(ωx+φ)的圖象與性質、兩角和與差的三角函數和反證法等知識,屬于中檔題.

 )|對一切x∈R恒成立,則
)|對一切x∈R恒成立,則 )=0; ②|f(
)=0; ②|f( )|<|f(
)|<|f( )|;
)|; ,kπ+
,kπ+ ](k∈Z);
](k∈Z); sin(2x+θ),結合已知不等式得f(
sin(2x+θ),結合已知不等式得f( )是函數的最大或最小值,從而得到
)是函數的最大或最小值,從而得到 sin(2x+
sin(2x+ +kπ)=±
+kπ)=± sin(2x+
sin(2x+ ).再根據三角函數y=Asin(ωx+φ)的圖象與性質,對各選項逐個加以判斷,可得①③⑤通過證明可得其正確性,而②④存在反例說明它們不正確.
).再根據三角函數y=Asin(ωx+φ)的圖象與性質,對各選項逐個加以判斷,可得①③⑤通過證明可得其正確性,而②④存在反例說明它們不正確. sin(2x+θ),其中角θ滿足cosθ=
sin(2x+θ),其中角θ滿足cosθ=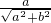 ,sinθ=
,sinθ=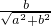
 )|對一切x∈R恒成立,
)|對一切x∈R恒成立, )=
)= 或-
或- ,得2×
,得2× +θ=
+θ= +kπ,k∈Z
+kπ,k∈Z +kπ,k∈Z.f(x)=
+kπ,k∈Z.f(x)= sin(2x+
sin(2x+ +kπ)=
+kπ)= sin(2x+
sin(2x+ )或-
)或- sin(2x+
sin(2x+ )
) +
+ )=sin2π=0,所以f(
)=sin2π=0,所以f( )=±
)=± sin(2×
sin(2× +
+ )=0,故①正確;
)=0,故①正確; )|=|
)|=| sin(2×
sin(2× +
+ )|=
)|=

 )|=|
)|=| sin(2×
sin(2× +
+ )|=
)|= sin
sin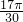 <
<

 )|>|f(
)|>|f( )|,故②不正確;
)|,故②不正確; sin(2x+
sin(2x+ )或-
)或- sin(2x+
sin(2x+ ),
), ,kπ+
,kπ+ ](k∈Z)不一定是增區間,故④不正確;
](k∈Z)不一定是增區間,故④不正確; ,平方得b2>a2+b2矛盾,故假設不成立
,平方得b2>a2+b2矛盾,故假設不成立

 星級口算天天練系列答案
星級口算天天練系列答案 (n∈N*)
(n∈N*) .
. 對不小于2的正整數恒成立,求x的取值范圍.
對不小于2的正整數恒成立,求x的取值范圍.