
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 方程的解所在的區間,則對應的函數的零點在這個范圍,把原函數寫出兩個初等函數,即兩個初等函數的交點在這個區間,結合兩個函數的草圖得到函數的交點的位置在(1,3),再進行進一步檢驗.
解答 解:∵方程log3x=-x+3的解,
根據兩個基本函數的圖象可知兩個函數的交點一定在(1,3),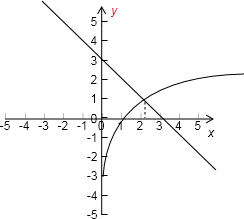
因m(x)=log3x+x-3在(1,2)上不滿足m(1)m(2)<0,
方程 log3x+x-3=0 的解所在的區間是(2,3),
即則x0所在的區間是(2,3),
故選:C.
點評 本題考查函數零點的檢驗,考查函數與對應的方程之間的關系,是一個比較典型的函數的零點的問題,注意解題過程中數形結合思想的應用.屬基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
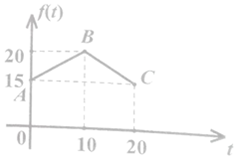 經過市場調查,某門市部的一種小商品在過去的20天內的銷售量(件)與價格(元)均為時間t (天)的函數,且日銷售量近似滿足g(t)=80-2t (件),而日銷售量價格近似滿足函數f(t),且f(t)的圖象為如圖所示的兩線段AB,BC.
經過市場調查,某門市部的一種小商品在過去的20天內的銷售量(件)與價格(元)均為時間t (天)的函數,且日銷售量近似滿足g(t)=80-2t (件),而日銷售量價格近似滿足函數f(t),且f(t)的圖象為如圖所示的兩線段AB,BC.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com