
【題目】(本題滿分14分)已知函數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 在其定義域上是增函數(shù),求實數(shù)
在其定義域上是增函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,求出
時,求出![]() 的極值;
的極值;
(Ⅲ)在(Ⅰ)的條件下,若![]() 在
在![]() 內(nèi)恒成立,試確定
內(nèi)恒成立,試確定![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)實數(shù)![]() 的取值范圍是
的取值范圍是![]() ;
;
(Ⅱ)極大值![]() ,極小值
,極小值![]() ;(Ⅲ),
;(Ⅲ),![]() 的取值范圍是
的取值范圍是![]() .
.
【解析】試題分析:(Ⅰ)首先求出函數(shù)![]() 的導函數(shù),再由函數(shù)
的導函數(shù),再由函數(shù)![]() 的單調(diào)性得到
的單調(diào)性得到![]() 在
在![]() 內(nèi)恒成立,最后由分離參數(shù)法求出實數(shù)
內(nèi)恒成立,最后由分離參數(shù)法求出實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)根據(jù)導函數(shù)的符號確定函數(shù)![]() 的單調(diào)區(qū)間與極值點,進而求出函數(shù)的極大值與極小值.
的單調(diào)區(qū)間與極值點,進而求出函數(shù)的極大值與極小值.
(Ⅲ)設![]() ,則
,則![]() 在
在![]() 內(nèi)恒成立
內(nèi)恒成立
等價于![]() 結合(I)的結果,利用導數(shù)判斷函數(shù)
結合(I)的結果,利用導數(shù)判斷函數(shù)![]() 的單調(diào)性,并出其最大值,從而求出
的單調(diào)性,并出其最大值,從而求出![]() 的取值范圍.
的取值范圍.
試題解析:
(Ⅰ)解:函數(shù)![]() 的定義域為
的定義域為![]() ,
,
則![]() ,
, ![]() 1分
1分
因為函數(shù)![]() 在
在![]() 內(nèi)是增函數(shù),
內(nèi)是增函數(shù),
所以![]() 在
在![]() 內(nèi)恒成立 2分
內(nèi)恒成立 2分
所以, ![]() 在
在![]() 內(nèi)恒成立 3分
內(nèi)恒成立 3分
因為當![]() 時,
時, ![]() ,當且僅當
,當且僅當![]() ,即
,即![]() 時, 等號成立,
時, 等號成立,
所以實數(shù)![]() 的取值范圍是
的取值范圍是![]() . 5分
. 5分
(Ⅱ)解:當![]() 時,
時, ![]() 7分
7分
當![]() 變化時,
變化時, ![]() ,
, ![]() 的變化情況如下:
的變化情況如下:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 遞增 | 極大值 | 遞減 | 極小值 | 遞增 |
所以, ![]() 在
在![]() 處取得極大值
處取得極大值![]() ,
,
![]() 在
在![]() 處取得極小值
處取得極小值![]() . 9分
. 9分
(Ⅲ)解:設![]()
![]() 10分
10分
則![]() 11分
11分
由(I)可知![]() ,且
,且![]() ,故
,故![]() ,
,
所以![]() 在
在![]() 內(nèi)為增函數(shù) 12分
內(nèi)為增函數(shù) 12分
因為![]() ,即
,即![]() ,
,
所以,![]() 的取值范圍是
的取值范圍是![]() 14分
14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】 由經(jīng)驗得知,在某商場付款處排隊等候付款的人數(shù)及概率如下表
排隊人數(shù) | 0 | 1 | 2 | 3 | 4 | 5人以上 |
概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(1)至多有2人排隊的概率是多少?
(2)至少有2人排隊的概率是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】曲線C:ρ2﹣2ρcosθ﹣8=0 曲線E: ![]() (t是參數(shù))
(t是參數(shù))
(1)求曲線C的普通方程,并指出它是什么曲線.
(2)當k變化時指出曲線K是什么曲線以及它恒過的定點并求曲線E截曲線C所得弦長的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,底面ABCD為正方形,平面AED⊥平面ABCD,AB= ![]() EA=
EA= ![]() ED,EF∥BD
ED,EF∥BD 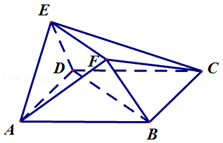
(I)證明:AE⊥CD
(II)在棱ED上是否存在點M,使得直線AM與平面EFBD所成角的正弦值為 ![]() ?若存在,確定點M的位置;若不存在,請說明理由.
?若存在,確定點M的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)的圖象與函數(shù)h(x)=x+![]() +2的圖象關于點A(0,1)對稱.
+2的圖象關于點A(0,1)對稱.
(1)求函數(shù)f(x)的解析式;
(2)若g(x)=f(x)+![]() ,g(x)在區(qū)間(0,2]上的值不小于6,求實數(shù)a的取值范圍.
,g(x)在區(qū)間(0,2]上的值不小于6,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】有一個偶數(shù)組成的數(shù)陣排列如下:
2 4 8 14 22 32 …
6 10 16 24 34 … …
12 18 26 36 … … …
20 28 38 … … … …
30 40 … … … … …
42 … … … … … …
… … … … … … …
則第20行第4列的數(shù)為( )
A. 546 B. 540 C. 592 D. 598
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=(x﹣b)lnx+x2在區(qū)間[1,e]上單調(diào)遞增,則實數(shù)b的取值范圍是( )
A.(﹣∞,﹣3]
B.(﹣∞,2e]
C.(﹣∞,3]
D.(﹣∞,2e2+2e]
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com