Question

已知長方體ABCD-A₁B₁C₁D₁中，AB=2，BC=1，AA₁=2，點M、N、P分別是棱AB、BC、DD₁上的點，

（1）若DP=DD₁，且PB⊥面MNB₁，求二面角M-B₁N-B的大小；

（2）棱DD₁上是否存在點P，使面APC₁⊥面ACC₁，證明你的結(jié)論.

Answer 1

思路分析：將立體幾何問題轉(zhuǎn)化為空間向量問題來解決.

解：(1）如圖建立直角坐標(biāo)系，則A（1,0,0），B（1,2,0），C（0,2,0），C₁（0,2,2），P（0,0,）.

∴=（-1,-2,），=（1,-2,0），=（0,0,2）.

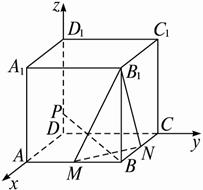
∵BP⊥面MNB₁，∴=（-1,-2,）為面MNB₁的法向量.

    又∵面BNB₁的單位法向量e=（0,1,0），

∴cos〈，e〉==-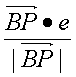

∴〈，e〉=π-arccos,

    即二面角M-B₁N-B的大小為π-arc cos.

(2）設(shè)面APC₁⊥面ACC₁，P（0,0,a）.作CH⊥AC₁，垂足為H.

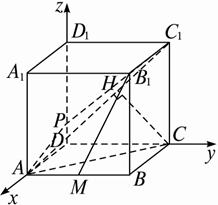
∵A、H、C₁三點共線，

∴+(1-λ)=λ(1,-2,0)+(1-λ)(0,0,2)=(λ,-2λ,2-2λ).

∵CH⊥AC₁，∴·=（λ,-2λ,2-2λ)·（-1,2,2）=0.

∴λ=.∴=(）.

∵面APC₁⊥面ACC₁，CH⊥AC₁，

∴CH⊥面APC₁,∴CH⊥AP.

∴=()·(-1,0,a)=0.∴a=.

∴存在點P（0,0,），使面APC₁⊥面ACC₁.

方法歸納 建立空間直角坐標(biāo)系是運用向量法解題的基本手段之一，往往用于圖形中存在互相垂直且相交的直線的前提下，如長方體、正方體.