
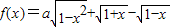 的最大值為g(a).
的最大值為g(a).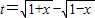 ,求t的取值范圍,并把f(x)表示為t的函數m(t);
,求t的取值范圍,并把f(x)表示為t的函數m(t);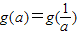 的所有實數a.
的所有實數a.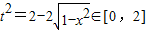 且定義域-1≤x≤1,易求得t的取值范圍,且
且定義域-1≤x≤1,易求得t的取值范圍,且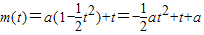 ,
,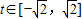
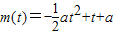 ,
,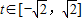 的最大值.結合二次函數圖象與性質,分類討論的方法求解.
的最大值.結合二次函數圖象與性質,分類討論的方法求解.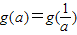 化為具體方程,須利用分段函數的知識,分a,
化為具體方程,須利用分段函數的知識,分a,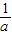 的范圍進行分類討論.
的范圍進行分類討論.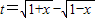 ,
,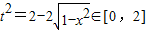 ①
①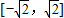 .(2分)
.(2分)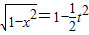 ,
,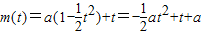 ,
,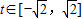 .(4分)
.(4分)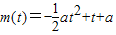 ,
,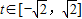 的最大值.
的最大值.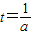 是拋物線
是拋物線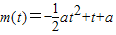 的對稱軸,
的對稱軸,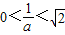 ,即
,即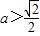 時,
時,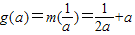 .(5分)
.(5分)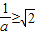 ,即
,即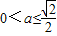 時,
時,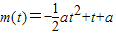
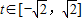 單調遞增,
單調遞增,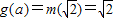 .(6分)
.(6分)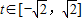 ,
,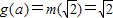 .(7分)
.(7分) (8分)
(8分)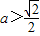 ,且
,且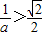 時,即
時,即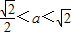 時,由
時,由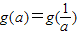 ,
,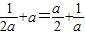 ,解得a=1.(9分)
,解得a=1.(9分)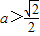 ,且
,且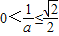 時,即
時,即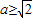 時,由
時,由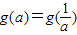 ,
,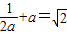 ,解得
,解得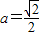 (舍) (10分)
(舍) (10分)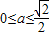 ,且
,且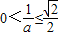 時,即a∈φ時,
時,即a∈φ時,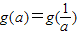 不成立.
不成立.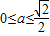 ,且
,且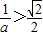 時,即
時,即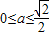 時,由
時,由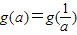 ,
, ,解得
,解得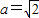 (舍)
(舍)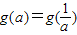 .(12分)
.(12分)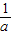 分別與0,
分別與0, 的大小關系.
的大小關系. 

 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:高中數學 來源: 題型:
| f(x) | a |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com