
【題目】在平面直角坐標(biāo)系中,已知雙曲線![]() 分別為
分別為![]() 的左,右頂點.
的左,右頂點.
(1)以![]() 為圓心的圓與
為圓心的圓與![]() 恰有三個不同的公共點,寫出此圓的方程;
恰有三個不同的公共點,寫出此圓的方程;
(2)直線![]() 過點
過點![]() ,與
,與![]() 在第一象限有公共點
在第一象限有公共點![]() ,線段
,線段![]() 的垂直平分線過點
的垂直平分線過點![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)![]() 上是否存在異于
上是否存在異于![]() 點
點![]() ,使
,使![]() 成立,若存在,求出所有
成立,若存在,求出所有![]() 的坐標(biāo),若不存在說明理由.
的坐標(biāo),若不存在說明理由.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)不存在,理由見解析
;(3)不存在,理由見解析
【解析】
(1)求雙曲線的左右頂點,可得以A為圓心的圓經(jīng)過B,求得半徑![]() ,可得所求圓的方程(2)設(shè)直線l的方程為
,可得所求圓的方程(2)設(shè)直線l的方程為![]() ,(
,(![]() ),聯(lián)立雙曲線方程,運用韋達(dá)定理,可得P的坐標(biāo),由中點坐標(biāo)公式可得AP的中點坐標(biāo),再由兩直線垂直的條件,解方程可得
),聯(lián)立雙曲線方程,運用韋達(dá)定理,可得P的坐標(biāo),由中點坐標(biāo)公式可得AP的中點坐標(biāo),再由兩直線垂直的條件,解方程可得![]() ,進(jìn)而得到所求直線方程(3)假設(shè)l上存在異于A,B點M,N,使
,進(jìn)而得到所求直線方程(3)假設(shè)l上存在異于A,B點M,N,使![]() 成立,設(shè)
成立,設(shè)![]() ,運用向量的坐標(biāo)表示和點滿足雙曲線方程,解方程可得M的坐標(biāo),即可判斷是否存在.
,運用向量的坐標(biāo)表示和點滿足雙曲線方程,解方程可得M的坐標(biāo),即可判斷是否存在.
(1)因為雙曲線為 ![]()
所以左右頂點![]() ,
,
由題意可得以A為圓心的圓經(jīng)過B,
則圓的半徑![]() ,圓的方程為
,圓的方程為![]() .
.
(2)直線![]() 過點
過點![]() ,且直線的斜率存在,
,且直線的斜率存在,
設(shè)直線![]() 的方程為
的方程為![]() ,
,
聯(lián)立雙曲線方程消去y,可得![]() ,
,
可得![]() ,可得
,可得![]() ,
,
可得![]() 的中點
的中點![]() 坐標(biāo)為
坐標(biāo)為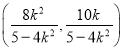 ,
,
由題意可得![]() ,即為
,即為![]() ,解得
,解得![]() (負(fù)的舍去),
(負(fù)的舍去),
則直線的方程為![]() ;
;
(3)設(shè)![]() ,
,
因為![]() ,
,
所以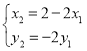
把![]() 代入雙曲線方程得:
代入雙曲線方程得:
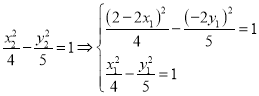
![]() ,與
,與![]() 點重合,故不存在.
點重合,故不存在.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某飲料生產(chǎn)企業(yè)為了占有更多的市場份額,擬在2017年度進(jìn)行一系列促銷活動,經(jīng)過市場調(diào)查和測算,飲料的年銷售量x萬件與年促銷費t萬元間滿足![]() .已知2017年生產(chǎn)飲料的設(shè)備折舊,維修等固定費用為3萬元,每生產(chǎn)1萬件飲料需再投入32萬元的生產(chǎn)費用,若將每件飲料的售價定為其生產(chǎn)成本的150%與平均每件促銷費的一半之和,則該年生產(chǎn)的飲料正好能銷售完.
.已知2017年生產(chǎn)飲料的設(shè)備折舊,維修等固定費用為3萬元,每生產(chǎn)1萬件飲料需再投入32萬元的生產(chǎn)費用,若將每件飲料的售價定為其生產(chǎn)成本的150%與平均每件促銷費的一半之和,則該年生產(chǎn)的飲料正好能銷售完.
(1)將2017年的利潤y(萬元)表示為促銷費t(萬元)的函數(shù);
(2)該企業(yè)2017年的促銷費投入多少萬元時,企業(yè)的年利潤最大?
(注:利潤=銷售收入-生產(chǎn)成本-促銷費,生產(chǎn)成本=固定費用+生產(chǎn)費用)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某租車公司給出的財務(wù)報表如下:
年度 項目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接單量(單) | 14463272 | 40125125 | 60331996 |
油費(元) | 214301962 | 581305364 | 653214963 |
平均每單油費 | 14.82 | 14.49 | |
平均每單里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投資者在研究上述報表時,發(fā)現(xiàn)租車公司有空駛情況,并給出空駛率的計算公式為![]() .
.
(1)分別計算2014,2015年該公司的空駛率的值(精確到0.01%);
(2)2016年該公司加強(qiáng)了流程管理,利用租車軟件,降低了空駛率并提高了平均每單里程,核算截止到11月30日,空駛率在2015年的基礎(chǔ)上降低了20個百分點,問2016年前11個月的平均每單油費和平均每單里程分別為多少?(分別精確到0.01元和0.01公里).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 由方程
由方程![]() 確定,下列結(jié)論正確的是________(請將你認(rèn)為正確的序號都填上)
確定,下列結(jié)論正確的是________(請將你認(rèn)為正確的序號都填上)
① ![]() 是
是![]() 上的單調(diào)遞減函數(shù);
上的單調(diào)遞減函數(shù);
② 對于任意![]() ,
,![]() 恒成立;
恒成立;
③ 對于任意![]() ,關(guān)于
,關(guān)于![]() 的方程
的方程![]() 都有解;
都有解;
④ ![]() 存在反函數(shù)
存在反函數(shù)![]() ,且對任意
,且對任意![]() ,總有
,總有![]() 成立.
成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .其中
.其中![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)求函數(shù)![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若不等式![]() 對任意的
對任意的![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】海洋藍(lán)洞是地球罕見的自然地理現(xiàn)象,被喻為“地球留給人類保留宇宙秘密的最后遺產(chǎn)”,我國擁有世界上最深的海洋藍(lán)洞,若要測量如圖所示的藍(lán)洞的口徑![]() ,
,![]() 兩點間的距離,現(xiàn)在珊瑚群島上取兩點
兩點間的距離,現(xiàn)在珊瑚群島上取兩點![]() ,
,![]() ,測得
,測得![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() 兩點的距離為___.
兩點的距離為___.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,長軸長為
,長軸長為![]() .
.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程及離心率;
的標(biāo)準(zhǔn)方程及離心率;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 滿足
滿足![]() ,求證:由點
,求證:由點![]() 構(gòu)成的曲線
構(gòu)成的曲線![]() 關(guān)于直線
關(guān)于直線![]() 對稱.
對稱.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
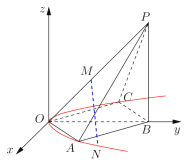
【題目】如圖,空間直角坐標(biāo)系中,四棱錐![]() 的底面是邊長為
的底面是邊長為![]() 的正方形,且底面在
的正方形,且底面在![]() 平面內(nèi),點
平面內(nèi),點![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 平面
平面![]() ,側(cè)棱
,側(cè)棱![]() 與底面所成角為45°;
與底面所成角為45°;
(1)若![]() 是頂點在原點,且過
是頂點在原點,且過![]() 、
、![]() 兩點的拋物線上的動點,試給出
兩點的拋物線上的動點,試給出![]() 與
與![]() 滿足的關(guān)系式;
滿足的關(guān)系式;
(2)若![]() 是棱
是棱![]() 上的一個定點,它到平面
上的一個定點,它到平面![]() 的距離為
的距離為![]() (
(![]() ),寫出
),寫出![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]() ,并求
,并求![]() 的最小值;
的最小值;
(3)是否存在一個實數(shù)![]() (
(![]() ),使得當(dāng)
),使得當(dāng)![]() 取得最小值時,異面直線
取得最小值時,異面直線![]() 與
與![]() 互相垂直?請說明理由;
互相垂直?請說明理由;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com