
 -
- =1,
=1, +
+ =1
=1 +
+ =1,
=1, +
+ =1.
=1. =
= =
= -1
-1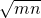
 -1=
-1=



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
| 2 | 7 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本小題滿分12分)已知雙曲線2x2-2y2=1的兩個焦點為F1,F2,P為動點,若|PF1|+|PF2|=4.
(1)求動點P的軌跡E的方程;
(2)求cos∠F1PF2的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源:2011年廣東省湛江市遂溪縣高考數(shù)學一模試卷(理科)(解析版) 題型:解答題
 ,0)作直線l交軌跡E于A、B兩點,判斷∠AMB的大小是否為定值?并證明你的結論.
,0)作直線l交軌跡E于A、B兩點,判斷∠AMB的大小是否為定值?并證明你的結論.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com