
如圖1,四棱錐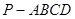 中,
中,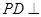 底面
底面 ,面
,面 是直角梯形,
是直角梯形,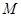 為側棱
為側棱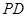 上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示.
上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示.
(1)證明: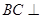 平面
平面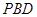 ;
;
(2)線段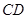 上是否存在點
上是否存在點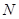 ,使
,使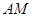 與
與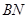 所成角的余弦值為
所成角的余弦值為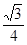 ?若存在,找到所有符合要求的點
?若存在,找到所有符合要求的點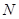 ,并求
,并求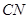 的長;若不存在,說明理由.
的長;若不存在,說明理由.
(1)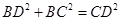 ,證得
,證得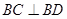 .又因為
.又因為  平面
平面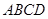 推出
推出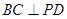 ,
,
又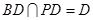 ,所以
,所以 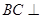 平面
平面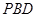 .
.
(2)點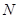 位于
位于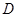 點處,此時
點處,此時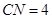 ;或
;或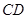 中點處,此時
中點處,此時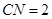 .
.
【解析】
試題分析:(1)【方法一】證明:由俯視圖可得,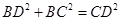 ,所以
,所以 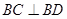 . 2分
. 2分
又因為  平面
平面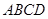 ,所以
,所以 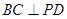 ,
4分
,
4分
又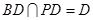 ,所以
,所以 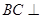 平面
平面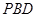 .
6分
.
6分
(1)【方法二】證明:因為 平面
平面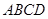 ,
,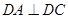 ,建立如圖所示
,建立如圖所示
的空間直角坐標系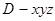 . 在△
. 在△ 中,易得
中,易得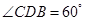 ,所以
,所以  ,
,

因為 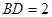 , 所以
, 所以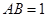 ,
, 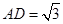 .由俯視圖和左視圖可得:
.由俯視圖和左視圖可得:
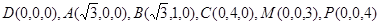 .
.
所以 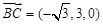 ,
,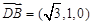 .
.
因為 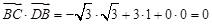 ,所以
,所以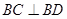 .
3分
.
3分
又因為  平面
平面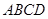 ,所以
,所以 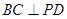 ,又
,又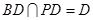
所以 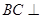 平面
平面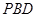 .
6分
.
6分
(2)解:線段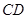 上存在點
上存在點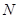 ,使
,使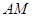 與
與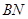 所成角的余弦值為
所成角的余弦值為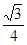 .
.
證明如下:設 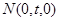 ,其中
,其中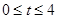 .
7分
.
7分
所以 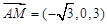 ,
,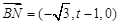 .
.
要使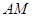 與
與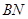 所成角的余弦值為
所成角的余弦值為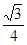 ,則有
,則有 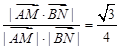 ,
9分
,
9分
所以 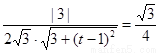 ,解得
,解得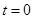 或
或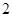 ,均適合
,均適合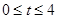 .
11分
.
11分
故點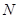 位于
位于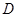 點處,此時
點處,此時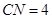 ;或
;或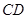 中點處,此時
中點處,此時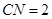 ,
12分
,
12分
考點:三視圖,立體幾何中的垂直關系、距離的計算。
點評:典型題,立體幾何題,是高考必考內容,往往涉及垂直關系、平行關系、角、距離、體積的計算。在計算問題中,有“幾何法”和“向量法”。利用幾何法,要遵循“一作、二證、三計算”的步驟,利用空間向量,省去繁瑣的證明,也是解決立體幾何問題的一個基本思路。注意運用轉化與化歸思想,將空間問題轉化成平面問題。本題將三視圖與證明、計算問題綜合考查,凸顯三視圖的基礎地位,必須正確還原幾何體。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:2012-2013學年北京市西城區(qū)高三二模理科數(shù)學試卷(解析版) 題型:解答題
如圖1,四棱錐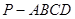 中,
中,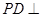 底面
底面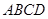 ,面
,面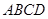 是直角梯形,
是直角梯形,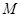 為側棱
為側棱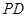 上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示.
上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示.
(Ⅰ)證明: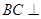 平面
平面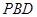 ;
;
(Ⅱ)證明: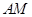 ∥平面
∥平面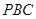 ;
;
(Ⅲ)線段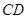 上是否存在點
上是否存在點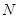 ,使
,使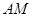 與
與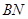 所成角的余弦值為
所成角的余弦值為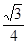 ?若存在,找到所有符合要求的點
?若存在,找到所有符合要求的點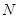 ,并求
,并求 的長;若不存在,說明理由.
的長;若不存在,說明理由.

查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年湖南省高三上學期第三次月考文科數(shù)學試卷(解析版) 題型:解答題
如圖,在四棱錐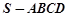 中,底面
中,底面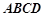 是直角梯形,
是直角梯形,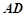 ∥
∥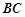 ,
,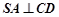 ,
, ⊥平面SAD,點
⊥平面SAD,點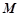 是
是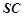 的中點,且
的中點,且 ,
,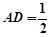 .
.

(1)求四棱錐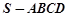 的體積;
的體積;
(2)求證: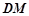 ∥平面
∥平面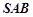 ;
;
(3)求直線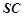 和平面
和平面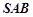 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源:河北省保定市高二年級第二學期期中聯(lián)考數(shù)學試卷(文科) 題型:解答題
如圖,在四棱錐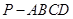 中,底面
中,底面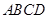 為菱形,
為菱形,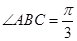 ,
, 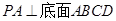 ,
, 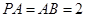 ,
,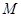 為
為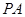 的中點,
的中點, 為
為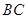 的中點
的中點
(1)證明:直線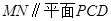
 ;
;
(2)求異面直線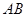 與
與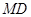 所成角的大小;
所成角的大小;
(3)求點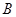 到平面
到平面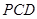 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年江蘇省高三第二次模擬考試數(shù)學試卷 題型:解答題
如圖,在四棱錐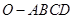 中,底面
中,底面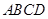 是邊長為1的菱形,
是邊長為1的菱形,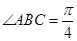 ,
, 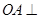 底面
底面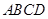 ,
,  ,
, 為
為 的中點.
的中點.
(Ⅰ)、求異面直線AB與MD所成角的大小;
(Ⅱ)、求平面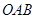 與平面
與平面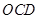 所成的二面角的余弦值.
所成的二面角的余弦值.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com