
已知數列的前n項和為Sn,并且滿足a1=2,nan+1=Sn+n(n+1).
(1)求{an}的通項公式;
(2)令Tn=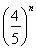 Sn,是否存在正整數m,對一切正整數n,總有Tn≤Tm?若存在,求m的值;若不存在,說明理由.
Sn,是否存在正整數m,對一切正整數n,總有Tn≤Tm?若存在,求m的值;若不存在,說明理由.
(1)an=2n.(2)m=8或m=9
【解析】(1)令n=1,由a1=2及nan+1=Sn+n(n+1),①得a2=4,故a2-a1=2,
當n≥2時,有(n-1)an=Sn-1+n(n-1),②
①-②,得nan+1-(n-1)an=an+2n.整理得an+1-an=2(n≥2).
當n=1時,a2-a1=2,所以數列{an}是以2為首項,以2為公差的等差數列,
故an=2+(n-1)×2=2n.
(2)由(1)得Sn=n(n+1),所以Tn=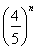 (n2+n).
(n2+n).
故Tn+1=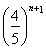 [(n+1)2+(n+1)],令
[(n+1)2+(n+1)],令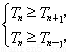
即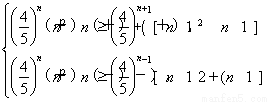 即
即
解得8≤n≤9.故T1<T2<…<T8=T9>T10>T11>…
故存在正整數m對一切正整數n,總有Tn≤Tm,
此時m=8或m=9


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第5課時練習卷(解析版) 題型:填空題
某科研單位欲拿出一定的經費獎勵科研人員,第1名得全部資金的一半多一萬元,第2名得剩下的一半多一萬元,以名次類推都得到剩下的一半多一萬元,到第10名恰好資金分完,則此科研單位共拿出________萬元資金進行獎勵.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第3課時練習卷(解析版) 題型:解答題
已知等比數列{an}中,a2=32,a8=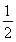 ,an+1<an.
,an+1<an.
(1)求數列{an}的通項公式;
(2)設Tn=log2a1+log2a2+…+log2an,求Tn的最大值及相應的n值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第2課時練習卷(解析版) 題型:解答題
已知在等差數列{an}中,a1=31,Sn是它的前n項和,S10=S22.
(1)求Sn;
(2)這個數列的前多少項的和最大,并求出這個最大值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第2課時練習卷(解析版) 題型:解答題
設等差數列{an}的前n項和為Sn,已知a3=5,S3=9.
(1)求首項a1和公差d的值;
(2)若Sn=100,求n的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第1課時練習卷(解析版) 題型:填空題
設Sn為數列{an}的前n項和,若Sn=(-1)nan-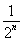 ,n∈N?,則a3=________.
,n∈N?,則a3=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第五章第1課時練習卷(解析版) 題型:解答題
已知數列{an}的前n項和Sn,求通項an.
(1)Sn=3n-1;
(2)Sn=n2+3n+1.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第9課時練習卷(解析版) 題型:填空題
對于任意的x1、x2∈(0,+∞),若函數f(x)=lgx,則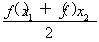 與f
與f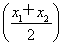 的大小關系是______________________.
的大小關系是______________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com