過直線y=x上的一點P作圓(x-5)2+(y-1)2=2的兩條切線l1,l2,A,B為切點,當直線l1,l2關于直線y=x對稱時,則∠APB=( )
A.30°
B.45°
C.60°
D.90°
【答案】
分析:判斷圓心與直線的關系,在直線上求出特殊點,P的方程,利用切線長、半徑以及該點與圓形連線構成直角三角形,求出∠APB的值.
解答:解:顯然圓心(5,1)不在直線y=x上.
由對稱性可知,只有直線y=x上的特殊點,這個點與圓心連線垂直于直線y=x,從這點做切線才能關于直線y=x對稱.
所以該點與圓形連線所在的直線方程為:y-5=-(x-1)即 y=6-x
與 y=x聯立可求出該點坐標為(3,3),
所以該點到圓心的距離為((5-3)
2+(1-3)
2=2
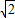
切線長、半徑以及該點與圓形連線構成直角三角形,又知圓的半徑為
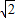
.
所以夾角的一半的正弦值為
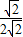
=

所以夾角∠APB=60°
故選C.
點評:本題是中檔題,考查直線與圓的位置關系,直線與圓相切的關系的應用,考查計算能力,常考題型.

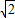
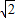 .
.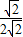 =
=


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案