
【題目】已知函數y=f(x)是R上的偶函數,當x1 , x2∈(0,+∞)時,都有(x1﹣x2)[f(x1)﹣f(x2)]<0.設 ![]() ,則( )
,則( )
A.f(a)>f(b)>f(c)
B.f(b)>f(a)>f(c)
C.f(c)>f(a)>f(b)
D.f(c)>f(b)>f(a)
科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AD∥BC, AB⊥BC, BD⊥DC,點E是BC邊的中點,將△ABD沿BD折起,使平面ABD⊥平面BCD,連接AE, AC, DE,得到如圖所示的空間幾何體.


(1)求證:AB⊥平面ADC;
(2)若AD=1,AB=![]() ,求點B到平面ADE的距離.
,求點B到平面ADE的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA= ![]() .
. 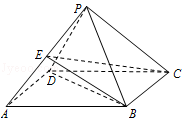
(Ⅰ)求證:BD⊥PC;
(Ⅱ)若E是PA的中點,求三棱錐P﹣BCE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空中有一氣球,在它的正西方A點測得它的仰角為45°,同時在它南偏東60°的B點,測得它的仰角為30°,已知A、B兩點間的距離為107米,這兩個觀測點均離地1米,則測量時氣球離地的距離是_____米.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知M( ![]() ,0),N(2,0),曲線C上的任意一點P滿足:
,0),N(2,0),曲線C上的任意一點P滿足: ![]()
![]() =
= ![]() |
| ![]() |.
|.
(Ⅰ)求曲線C的方程;
(Ⅱ)設曲線C與x軸的交點分別為A、B,過N的任意直線(直線與x軸不重合)與曲線C交于R、Q兩點,直線AR與BQ交于點S.問:點S是否在同一直線上?若是,請求出這條直線的方程;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某公司舉行的年終慶典活動中,主持人利用隨機抽獎軟件進行抽獎:由電腦隨機生成一張如圖所示的3![]() 3表格,其中1格設獎300元,4格各設獎200元,其余4格各設獎100元,點擊某一格即顯示相應金額.某人在一張表中隨機不重復地點擊3格,記中獎的總金額為X元.
3表格,其中1格設獎300元,4格各設獎200元,其余4格各設獎100元,點擊某一格即顯示相應金額.某人在一張表中隨機不重復地點擊3格,記中獎的總金額為X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及數學期望
的概率分布及數學期望![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A市某機構為了調查該市市民對我國申辦2034年足球世界杯的態度,隨機選取了140位市民進行調查,調查結果統計如下:
支持 | 不支持 | 總計 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合計 | 70 | 140 |
(I)根據已知數據,把表格數據填寫完整;
(II)利用(1)完成的表格數據回答下列問題:
(ⅰ)能否在犯錯誤的概率不超過0.001的前提下認為性別與支持申辦足球世界杯有關;
(ⅱ)已知在被調查的支持申辦足球世界杯的男性市民中有5位退休老人,其中2位是教師,現從這5位退休老人中隨機抽取3人,求至多有1位老師的概率。
附:![]() ,其中
,其中![]()
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的左、右焦點分別為F1 , F2 , O為坐標原點,點P(1,
=1(a>b>0)的左、右焦點分別為F1 , F2 , O為坐標原點,點P(1, ![]() )在橢圓上,連接PF1交y軸于點Q,點Q滿足
)在橢圓上,連接PF1交y軸于點Q,點Q滿足 ![]() =
= ![]() .直線l不過原點O且不平行于坐標軸,l與橢圓C有兩個交點A,B. (Ⅰ)求橢圓C的標準方程;
.直線l不過原點O且不平行于坐標軸,l與橢圓C有兩個交點A,B. (Ⅰ)求橢圓C的標準方程;
(Ⅱ)已知點M( ![]() ,0),若直線l過橢圓C的右焦點F2 , 證明:
,0),若直線l過橢圓C的右焦點F2 , 證明: ![]()
![]() 為定值;
為定值;
(Ⅲ)若直線l過點(0,2),設N為橢圓C上一點,且滿足 ![]() +
+ ![]() =λ
=λ ![]() ,求實數λ的取值范圍.
,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an},{bn}滿足 ![]() ,
, ![]() ,其中n∈N+ . (I)求證:數列{bn}是等差數列,并求出數列{an}的通項公式;
,其中n∈N+ . (I)求證:數列{bn}是等差數列,并求出數列{an}的通項公式;
(II)設 ![]() ,求數列{cncn+2}的前n項和為Tn .
,求數列{cncn+2}的前n項和為Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com