
【題目】已知圓C的圓心在坐標原點,且與直線l1:x﹣y﹣2 ![]() =0相切 (Ⅰ)求直線l2:4x﹣3y+5=0被圓C所截得的弦AB的長.
=0相切 (Ⅰ)求直線l2:4x﹣3y+5=0被圓C所截得的弦AB的長.
(Ⅱ)過點G(1,3)作兩條與圓C相切的直線,切點分別為M,N,求直線MN的方程
(Ⅲ) 若與直線l1垂直的直線l與圓C交于不同的兩點P,Q,若∠POQ為鈍角,求直線l縱截距的取值范圍.
【答案】解:(Ⅰ)由題意得:圓心(0,0)到直線l1:x﹣y﹣2 ![]() 的距離為圓的半徑, r=
的距離為圓的半徑, r= ![]() =2,所以圓C的標準方程為:x2+y2=4,
=2,所以圓C的標準方程為:x2+y2=4,
所以圓心到直線l2的距離d= ![]()
∴ ![]()
(Ⅱ)因為點G(1,3),所以 ![]() ,
, ![]()
所以以G點為圓心,線段GM長為半徑的圓G方程:(x﹣1)2+(y﹣3)2=6 (1)
又圓C方程為:x2+y2=4 (2),由(1)﹣(2)得直線MN方程:x+3y﹣4=0
(Ⅲ)設直線l的方程為:y=﹣x+b聯立x2+y2=4得:2x2﹣2bx+b2﹣4=0,
設直線l與圓的交點P(x1 , y1),Q(x2 , y2),
由△=(﹣2b)2﹣8(b2﹣4)>0,得b2<8,x1+x2=b, ![]() (3)
(3)
因為∠POQ為鈍角,所以 ![]() ,
,
即滿足x1x2+y1y2<0,且 ![]() 與
與 ![]() 不是反向共線,
不是反向共線,
又y1=﹣x1+b,y2=﹣x2+b所以 ![]()
由(3)(4)得b2<4,滿足△>0,即﹣2<b<2,
當 ![]() 與
與 ![]() 反向共線時,直線y=﹣x+b過原點,此時b=0,不滿足題意,
反向共線時,直線y=﹣x+b過原點,此時b=0,不滿足題意,
故直線l縱截距的取值范圍是﹣2<b<2,且b≠0
【解析】(Ⅰ)由直線與圓相交的性質可知,( ![]() )2=r2﹣d2 , 要求AB,只要求解圓心到直線4x﹣3y+5=0的距離.即可求直線l2:4x﹣3y+5=0被圓C所截得的弦AB的長.(Ⅱ)求出圓C的方程以及以G(1,3)為圓心,QM為半徑的圓,利用圓系方程求直線MN的方程.(Ⅲ)設直線l的方程為:y=﹣x+b聯立x2+y2=4,設直線l與圓的交點P(x1 , y1),Q(x2 , y2),利用△>0,以及韋達定理,通過∠POQ為鈍角,求出﹣2<b<2,當
)2=r2﹣d2 , 要求AB,只要求解圓心到直線4x﹣3y+5=0的距離.即可求直線l2:4x﹣3y+5=0被圓C所截得的弦AB的長.(Ⅱ)求出圓C的方程以及以G(1,3)為圓心,QM為半徑的圓,利用圓系方程求直線MN的方程.(Ⅲ)設直線l的方程為:y=﹣x+b聯立x2+y2=4,設直線l與圓的交點P(x1 , y1),Q(x2 , y2),利用△>0,以及韋達定理,通過∠POQ為鈍角,求出﹣2<b<2,當 ![]() 與
與 ![]() 反向共線時,直線y=﹣x+b過原點,此時b=0,不滿足題意,即可得到結果.
反向共線時,直線y=﹣x+b過原點,此時b=0,不滿足題意,即可得到結果.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn , 已知a3=24,a6=18.
(Ⅰ) 求數列{an}的通項公式;
(Ⅱ)求數列{an}的前n項和Sn;
(Ⅲ)當n為何值時,Sn最大,并求Sn的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的污水處理程序如下:原始污水必先經過A系統處理,處理后的污水(A級水)達到環保標準(簡稱達標)的概率為![]() .經化驗檢測,若確認達標便可直接排放;若不達標則必須進行B系統處理后直接排放.
.經化驗檢測,若確認達標便可直接排放;若不達標則必須進行B系統處理后直接排放.
某廠現有![]() 個標準水量的A級水池,分別取樣、檢測. 多個污水樣本檢測時,既可以逐個化驗,也可以將若干個樣本混合在一起化驗.混合樣本中只要有樣本不達標,則混合樣本的化驗結果必不達標.若混合樣本不達標,則該組中各個樣本必須再逐個化驗;若混合樣本達標,則原水池的污水直接排放.
個標準水量的A級水池,分別取樣、檢測. 多個污水樣本檢測時,既可以逐個化驗,也可以將若干個樣本混合在一起化驗.混合樣本中只要有樣本不達標,則混合樣本的化驗結果必不達標.若混合樣本不達標,則該組中各個樣本必須再逐個化驗;若混合樣本達標,則原水池的污水直接排放.
現有以下四種方案,
方案一:逐個化驗;
方案二:平均分成兩組化驗;
方案三:三個樣本混在一起化驗,剩下的一個單獨化驗;
方案四:混在一起化驗.
化驗次數的期望值越小,則方案的越“優”.
(Ⅰ) 若![]() ,求
,求![]() 個A級水樣本混合化驗結果不達標的概率;
個A級水樣本混合化驗結果不達標的概率;
(Ⅱ) 若![]() ,現有
,現有![]() 個A級水樣本需要化驗,請問:方案一,二,四中哪個最“優”?
個A級水樣本需要化驗,請問:方案一,二,四中哪個最“優”?
(Ⅲ) 若“方案三”比“方案四”更“優”,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 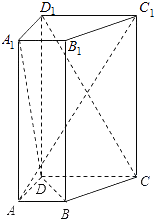
(1)求證:D1C⊥AC1;
(2)設E是DC上一點,試確定E的位置,使D1E∥平面A1BD,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設直線l的方程為(a+1)x+y+2﹣a=0(a∈R)
(1)若直線l在兩坐標軸上的截距相等,則直線l的方程是;
(2)若直線l不經過第二象限,則實數a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱ABC﹣A1B1C1中,側面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且點O為AC中點.
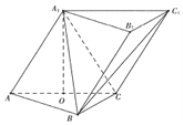
(Ⅰ)證明:A1O⊥平面ABC;
(Ⅱ)求三棱錐C1﹣ABC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2﹣2ax+b(a>0)在區間[﹣1,4]上有最大值10和最小值1.設g(x)= ![]() .
.
(1)求a、b的值;
(2)證明:函數g(x)在[ ![]() ,+∞)上是增函數;
,+∞)上是增函數;
(3)若不等式g(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求實數k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com