本題滿分12分，每小題各4分）
已知函數
，
（1）若函數
的值域為
，求實數a的值；
（2）若函數的遞增區間為，求實數a的值；
（3）若函數在區間上是增函數，求實數a的取值范圍．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源：2012-2013學年福建省高三第一次階段考試文科數學試卷（解析版） 題型：解答題
（本題滿分12分，每小題6分）
（1）若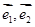
為基底向量，且
若A、B、D三點共線，求實數k的值；
（2）用“五點作圖法”在已給坐標系中畫出函數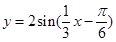
一個周期內的簡圖，并指出該函數圖象是由函數
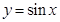的圖象進行怎樣的變換而得到的？
查看答案和解析>>
科目：高中數學 來源：2011-2012學年安徽省高三第二次聯考理科數學 題型：解答題
(本題滿分12分) 某皮制廠去年生產皮質小包的年產量為10萬件，每件皮質小包的銷售價格平均為100元，生產成本為80元.從今年起工廠投入100萬元科技成本，并計劃以后每年比上一年多投入100萬元科技成本，預計產量每年遞增1萬件.設第
年每件小包的生產成本
元，若皮制產品的銷售價格不變，第年的年利潤為
萬元（今年為第一年）.
（Ⅰ）求的表達式
（Ⅱ）問從今年算起第幾年的利潤最高？最高利潤為多少萬元？
查看答案和解析>>
科目：高中數學 來源：2010-2011學年方城一高高三年級10月月考數學試卷（理科） 題型：解答題
（本題滿分12分）為了在夏季降溫和冬季供暖時減少能源損耗，房屋的屋頂和外墻需要建造隔熱層．某幢建筑物要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元．該建筑物每年的能源消耗費用C（單位：萬元）與隔熱層厚度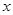
（單位：cm）滿足關系：
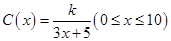，若不建隔熱層，每年能源消耗費用為8萬元．設
為隔熱層建造費用與20年的能源消耗費用之和．
（Ⅰ）求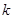
的值及的表達式；
（Ⅱ）隔熱層修建多厚對，總費用達到最小，并求最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（2）