Question

【題目】如圖已知橢圓C： +y2=1，以橢圓的左頂點T為圓心作圓T：（x+2）2+y2=r2（r＞0）．設圓T與橢圓C交于點M與點N．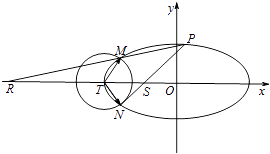
（1）求 的最小值；
（2）設點P是橢圓C上異于M，N的任意一點，且直線MP，NP分別與x軸交于點R，S，O為坐標原點，求證：丨OR丨丨OS丨為定值．

Answer 1

【答案】
（1）解：依題意，得a=2，b=1，c= = ，T（﹣2，0）．

點M與點N關于x軸對稱，

設M（x1，y1），N（x1，﹣y1），不妨設y1＞0．

由于點M在橢圓C上，∴ =1﹣ ，（*）

=（x1+2，y1）， =（x1+2，﹣y1），

∴ =（x1+2）2﹣

= = ﹣ ，

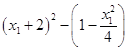由于﹣2＜x1＜2，

故當 時， 取得最小值為﹣

（2）證明：設P（x0，y0），

則直線MP的方程為：y﹣y0= （x﹣x0），

令y=0，得xR= ，

同理：xS= ，

故xRxS= ，（**）

又點M與點P在橢圓上，故 ， =4 ，

代入（**）式，得：xRxS= 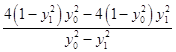= =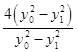4．

∴丨OR丨丨OS丨=|xRxS|=4為定值

【解析】（1）T（﹣2，0）．點M與點N關于x軸對稱，設M（x11），N（x1 ， ﹣y1），不妨設y1＞0．由于點M在橢圓C上， =1﹣ ，可得 = ﹣ ，由于﹣2＜x1＜2，可得 取得最小值．（2）設P（x0 ， y0），則直線MP的方程為：y﹣y0= （x﹣x0），令y=0，得xR= ，同理：xS= ，xRxS= ，又點M與點P在橢圓上，故 ， =4 ，代入丨OR丨丨OS丨=|xRxS|，化簡即可證明．