
設函數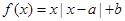 ,
,
(1)若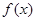 是奇函數,求a、b滿足的條件;
是奇函數,求a、b滿足的條件;
(2)若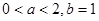 ,求
,求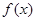 在區(qū)間[0,2]上的最大值
在區(qū)間[0,2]上的最大值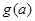 ;
;
(3)求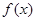 的單調區(qū)間.
的單調區(qū)間.
(1)a=0且b=0
(2)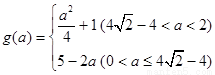
(3)單增區(qū)間有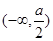 和
和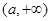 ,單減區(qū)間有
,單減區(qū)間有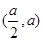
【解析】第一問中因為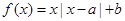 ,且
,且 是奇函數,所以f(0)=0
是奇函數,所以f(0)=0
第二問中,由圖像,最大值只能在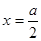 和
和 處取到
處取到
然后比較大小,確定最值。
第三問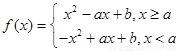 ,對于參數a進行討論得到單調區(qū)間。
,對于參數a進行討論得到單調區(qū)間。
解:(1解:因為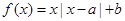 ,且
,且 是奇函數,所以f(0)=0
是奇函數,所以f(0)=0
a=0且b=0 -----------4
(2)由圖像,最大值只能在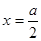 和
和 處取到
處取到
若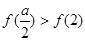 即
即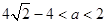 時,最大值
時,最大值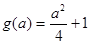
若 即
即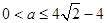 時,最大值
時,最大值
所以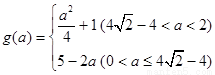 --------------10
--------------10
(3)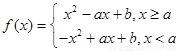
①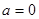 ,
,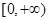
 單調遞增,
單調遞增, 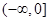
 單調遞增,所以在R上單調遞增
單調遞增,所以在R上單調遞增
②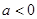 時
時
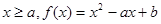 對稱軸
對稱軸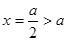 ,所以f(x)在
,所以f(x)在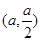 上單調減,f(x)在
上單調減,f(x)在 單調遞增
單調遞增
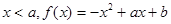 對稱軸
對稱軸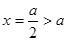 ,所以f(x)在
,所以f(x)在 上單調增
上單調增
所以,單增區(qū)間有 和
和 ,單減區(qū)間有
,單減區(qū)間有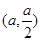
③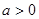 時
時
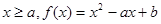 對稱軸
對稱軸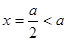 ,所以f(x)在
,所以f(x)在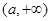 單調遞增
單調遞增
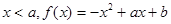 對稱軸
對稱軸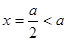 ,所以f(x)在
,所以f(x)在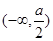 上單調增,f(x)在
上單調增,f(x)在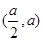 單調遞減
單調遞減
所以,單增區(qū)間有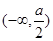 和
和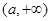 ,單減區(qū)間有
,單減區(qū)間有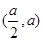 --------------16
--------------16


科目:高中數學 來源:2013-2014學年上海市長寧區(qū)高三上學期教學質量檢測理科數學試卷(解析版) 題型:解答題
已知函數 ,
,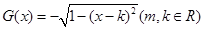
(1)若 是常數,問當
是常數,問當 滿足什么條件時,函數
滿足什么條件時,函數 有最大值,并求出
有最大值,并求出 取最大值時
取最大值時 的值;
的值;
(2)是否存在實數對 同時滿足條件:(甲)
同時滿足條件:(甲) 取最大值時
取最大值時 的值與
的值與 取最小值的
取最小值的 值相同,(乙)
值相同,(乙) ?
?
(3)把滿足條件(甲)的實數對 的集合記作A,設
的集合記作A,設 ,求使
,求使 的
的 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆浙江臺州高二下學期第一次月考理科數學試卷(解析版) 題型:解答題
設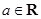 ,函數
,函數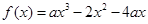 ,
,
(1)若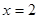 是函數
是函數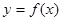 的極值點,求
的極值點,求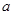 的值;
的值;
(2)在(1)的條件下,求函數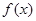 在區(qū)間
在區(qū)間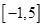 上的最值.
上的最值.
(3)是否存在實數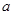 ,使得函數
,使得函數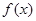 在
在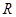 上為單調函數,若是,求出
上為單調函數,若是,求出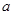 的取值范圍,若不是,請說明理由。
的取值范圍,若不是,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com