
【題目】已知![]() 為實數,用
為實數,用![]() 表示不超過
表示不超過![]() 的最大整數.
的最大整數.
(1)若函數![]() ,求
,求![]() 的值;
的值;
(2)若函數![]() ,求
,求![]() 的值域;
的值域;
(3)若存在![]() 且
且![]() ,使得
,使得![]() ,則稱函數
,則稱函數![]() 是
是![]() 函數,若函數
函數,若函數 ![]() 是
是![]() 函數,求
函數,求![]() 的取值范圍.
的取值范圍.
【答案】(1)1,2;(2){0,1};(3)![]() 且
且![]() 且
且![]() .
.
【解析】
(1)根據取整函數的定義直接計算;
(2)考慮![]() 與
與![]() 之間的大小關系,從而得到
之間的大小關系,從而得到![]() 的值域;
的值域;
(3)對![]() 進行分類討論:
進行分類討論:![]() ,利用單調性證明
,利用單調性證明![]() 在
在![]() 時不成立,當
時不成立,當![]() 時,再對
時,再對![]() 分類討論:
分類討論:![]() ,由此求解出
,由此求解出![]() 的取值范圍.
的取值范圍.
(1)f(1.2)=1,f(-1.2)=-2;
(2)因為[![]() ]=[
]=[![]() ]或[
]或[![]() ]=[
]=[![]() ]+1
]+1
所以若函數![]() 的值域為{0,1}
的值域為{0,1}
(3)當函數f(x)=x+![]() 是Ω函數時,
是Ω函數時,
若a=0,則f(x)=x顯然不是Ω函數,矛盾.
若a<0,則![]() 是一個增函數,
是一個增函數,
所以f(x)在(﹣∞,0),(0,+∞)上單調遞增,
此時不存在m<0,使得f(m)=f([m]),
同理不存在m>0,使得f(m)=f([m]),
又注意到m[m]≥0,即不會出現[m]<0<m的情形,
所以此時f(x)=x+![]() 不是Ω函數.
不是Ω函數.
當a>0時,設f(m)=f([m]),所以m+![]() =[m]+
=[m]+![]() ,所以有a=m[m],其中[m]≠0,
,所以有a=m[m],其中[m]≠0,
當m>0時,
因為[m]<m<[m]+1,所以[m]2<m[m]<([m]+1)[m],
所以[m]2<a<([m]+1)[m],
當m<0時,[m]<0,
因為[m]<m<[m]+1,所以[m]2>m[m]>([m]+1)[m],
所以[m]2>a>([m]+1)[m],
記k=[m],綜上,我們可以得到:a>0且k∈N,a≠k2且a≠k(k+1).


科目:高中數學 來源: 題型:
【題目】某紀念章從2018年10月1日起開始上市,通過市場調查,得到該紀念章每1枚的市場價(單位:元)與上市時間(單位:天)的數據如下:
上市時間 | 4 | 10 | 36 |
市場價 | 90 | 51 | 90 |
(1)根據上表數據,從下列函數中選取一個恰當的函數描述該紀念章的市場價![]() 與上市時間
與上市時間![]() 的變化關系并說明理由:①
的變化關系并說明理由:①![]() ;②
;②![]() ;③
;③![]() .
.
(2)利用你選取的函數,求該紀念章市場價最低時的上市天數及最低的價格.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,拋物線
,拋物線![]() 的焦點均在
的焦點均在![]() 軸上,
軸上,![]() 的中心和
的中心和![]() 的頂點均為坐標原點.下表給出坐標的五個點中,有兩個點在
的頂點均為坐標原點.下表給出坐標的五個點中,有兩個點在![]() 上,另有兩個點在
上,另有兩個點在![]() 上. 則橢圓
上. 則橢圓![]() 的方程為_____,
的方程為_____,![]() 的左焦點到
的左焦點到![]() 的準線之間的距離為_______.
的準線之間的距離為_______.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著“互聯網+交通”模式的迅猛發展,“共享助力單車”在很多城市相繼出現.某“共享助力單車”運營公司為了解某地區用戶對該公司所提供的服務的滿意度,隨機調查了100名用戶,得到用戶的滿意度評分(滿分10分),現將評分分為5組,如下表:
組別 | 一 | 二 | 三 | 四 | 五 |
滿意度評分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
頻數 | 5 | 10 | a | 32 | 16 |
頻率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估計用戶的滿意度評分的平均數;
(3)若從這100名用戶中隨機抽取25人,估計滿意度評分低于6分的人數為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,動物園要建造一面靠墻的2間面積相同的矩形熊貓居室,如果可供建造圍墻的材料總長是36m。

(1)把每間熊貓居室的面積s(單位:![]() )表示為寬x(單位:m)的函數,求函數的解析式,并寫出定義域;
)表示為寬x(單位:m)的函數,求函數的解析式,并寫出定義域;
(2)當寬為多少時才能使所建造的每間熊貓居室面積最大?每間熊貓居室最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年11月、12月全國大范圍流感爆發,為研究晝夜溫差大小與患感冒人數多少之間的關系,一興趣小組抄錄了某醫院11月到12月間的連續6個星期的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
日期 | 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | 第六周 |
晝夜溫差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數y(個) | 22 | 25 | 29 | 26 | 16 | 12 |
該興趣小組確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗。
(Ⅰ)求選取的2組數據恰好是相鄰兩個星期的概率;
(Ⅱ)若選取的是第一周與第六周的兩組數據,請根據第二周到第五周的4組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅲ)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
(參考公式: 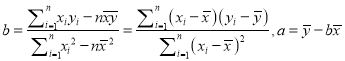 )
)
參考數據: ![]() 1092,
1092, ![]() 498
498
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com