
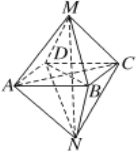
【題目】在棱長為![]() 的正方體
的正方體![]() 中,
中,![]() 分別是
分別是![]() 的中點,過
的中點,過![]() 三點的平面與正方體的下底面相交于直線
三點的平面與正方體的下底面相交于直線![]() ;
;

(1)畫出直線![]() ;
;
(2)設![]() 求
求![]() 的長;
的長;
(3)求D到![]() 的距離.
的距離.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據正方體的幾何特征,連接DM并延長交D1A1的延長線于Q.連接NQ,即可得到滿足條件的直線l;
(2)若l∩A1B1=P,即QN∩A1B1=P,易根據三角形全等的性質得到A1是QD1的中點.進而求出PB1的長;
(3)作D1H⊥l于H,連接DH,根據正方體的幾何特征,易得DH⊥l,即DH的長就是D到l的距離.解Rt△QD1N即可得到答案.
(1)連結DM并延長交D1A1的延長線于Q,連結NQ,則NQ所在直線即為所求的直線![]() .
.

(2)設QN![]() A1B1=P,∵AM=A1M,∠AMD=∠A1MQ, ∠DAM=∠QA1M,易證得
A1B1=P,∵AM=A1M,∠AMD=∠A1MQ, ∠DAM=∠QA1M,易證得![]() ,所以
,所以![]() ,即A1是QD1的中點.
,即A1是QD1的中點.
![]()
![]()
(3)作![]() 于H,連接
于H,連接![]() ,可證明
,可證明![]() ,
,
則![]() 的長就是D到
的長就是D到![]() 的距離.
的距離.
在![]() 中,兩直角邊
中,兩直角邊![]() ,
,![]() 斜邊QN=
斜邊QN=![]() .
.
所以![]() ,所以
,所以![]() ,
,![]()
即D到![]() 的距離為
的距離為![]() .
.


 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體,關于其結構特征,下列說法不正確的是
A. 該幾何體是由兩個同底的四棱錐組成的幾何體
B. 該幾何體有12條棱、6個頂點
C. 該幾何體有8個面,并且各面均為三角形
D. 該幾何體有9個面,其中一個面是四邊形,其余均為三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 、圓
、圓![]() 均滿足圓心在直線
均滿足圓心在直線![]() :
: ![]() 上,過點
上,過點![]() ,且與直線l2:x=-1相切.
,且與直線l2:x=-1相切.
(1)當![]() 時,求圓
時,求圓![]() ,圓
,圓![]() 的標準方程;
的標準方程;
(2)直線l2與圓![]() 、圓
、圓![]() 分別相切于A,B兩點,求
分別相切于A,B兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】齊王與田忌賽馬,田忌的上等馬優于齊王的中等馬,劣于齊王的上等馬,田忌的中等馬優于齊王的下等馬,劣于齊王的中等馬, 田忌的下等馬劣于齊王的下等馬.現從雙方的馬匹中隨機選一匹進行一場比賽,則田忌的馬獲勝的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com