Question

函數y=sin²x是（ ）
A．最小正周期為2π的偶函數
B．最小正周期為2π的奇函數
C．最小正周期為π的偶函數
D．最小正周期為π的奇函數

Answer 1

【答案】分析：首先由f（-x）=f（x）判斷函數為偶函數；利用二倍角的余弦化簡原式=-cos2x，根據求最小周期公式得出結論．
解答：解：函數f（x）=sin²x 則f（-x）=sin²（-x）=f（x）
∴函數y=sin²x為偶函數
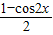
函數y=sin²x==-cos2x，
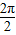
∴最小正周期為T==π，
故選C．
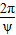
點評：本題考查二倍角公式、三角函數周期性的求法，求最小周期公式T=是解題關鍵，屬于基礎題．