
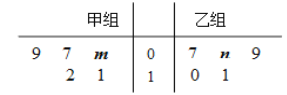
【題目】某車間將10名技工平均分成甲、乙兩組加工某種零件,在單位時間內每個技工加工的合格零件數的統計數據的莖葉圖如圖所示.已知兩組技工在單位時間內加工的合格零件平均數都為9.
(1)分別求出![]() 的值;
的值;
(2)分別求出甲、乙兩組技工在單位時間內加工的合格零件的方差![]() 和
和![]() ,并由此分析兩組技工的加工水平;
,并由此分析兩組技工的加工水平;
(3)質檢部門從該車間甲、乙兩組技工中各隨機抽取一名技工,對其加工的零件進行檢測,若兩人加工的合格零件個數之和大于17,則稱該車間“質量合格”,求該車間“質量合格”的概率.
【答案】(1)![]() (2)甲乙兩組的整體水平相當,乙組更穩定一些(3)
(2)甲乙兩組的整體水平相當,乙組更穩定一些(3)![]()
【解析】
試題分析:(1)由兩組技工在單位時間內加工的合格零件平均數都為9.利用莖葉圖能求出m,n;(2)先分別求出![]() ,
,![]() ,由兩組技工在單位時間內加工的合格零件平均數都為9,
,由兩組技工在單位時間內加工的合格零件平均數都為9,![]() ,得到乙組技工加工水平高;(3)質監部門從該車間甲、乙兩組技工中各隨機抽取一名技工,對其加工的零件進行檢測,設兩人加工的合格零件數分別為(a,b),利用列舉法能求出該車間“質量合格”的概率
,得到乙組技工加工水平高;(3)質監部門從該車間甲、乙兩組技工中各隨機抽取一名技工,對其加工的零件進行檢測,設兩人加工的合格零件數分別為(a,b),利用列舉法能求出該車間“質量合格”的概率
試題解析:(1)∵兩組技工在單位時間內加工的合格零件平均數都為9.
∴由莖葉圖得:![]() (9+7+m+11+12)=9
(9+7+m+11+12)=9
![]() (7+n+9+10+11)=9,
(7+n+9+10+11)=9,
解得m=6,n=8.------------------------------2
(2)![]() ,
,
![]() ,--------------4
,--------------4
∵![]() ,
,![]() ,∴甲乙兩組的整體水平相當,乙組更穩定一些;-------6
,∴甲乙兩組的整體水平相當,乙組更穩定一些;-------6
(3)由題意,基本事件空間
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,共計
,共計![]() 個,而
個,而![]() 的基本事件-----------8
的基本事件-----------8
A=![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
共計![]() 個基本事件,故滿足
個基本事件,故滿足![]() 的基本事件共有14,即該車間“質量合格”的基本事件有14個,----------------10
的基本事件共有14,即該車間“質量合格”的基本事件有14個,----------------10
故該車間“質量合格”的概率為![]() .---------------12
.---------------12


科目:高中數學 來源: 題型:
【題目】口袋內裝有大小相同的紅球、白球和黑球,從中摸出一個球,摸出紅球的概率是0.42,摸出白球的概率是0.28,則摸出黑球的概率是( )
A. 0.42 B. 0.28 C. 0.7 D. 0.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一醫用放射性物質原來質量為a,每年衰減的百分比相同,當衰減一半時,所用時間是10年,根據需要,放射性物質至少要保留原來的,否則需要更換.已知到今年為止,剩余的為原來的![]() ,
,
(1)求每年衰減的百分比;
(2)到今年為止,該放射性物質已衰減了多少年?
(3)今后至多還能用多少年?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位實行休年假制度三年以來,50名職工休年假的次數進行的調查統計結果如下表所示:
休假次數 | 0 | 1 | 2 | 3 |
人數 | 5 | 10 | 20 | 15 |
根據表中信息解答以下問題:
(1)從該單位任選兩名職工,用![]() 表示這兩人休年假次數之和,記“函數
表示這兩人休年假次數之和,記“函數![]() 在區間
在區間![]() 上有且只有一個零點”為事件
上有且只有一個零點”為事件![]() ,求事件
,求事件![]() 發生的概率
發生的概率![]() ;
;
(2)從該單位任選兩名職工,用![]() 表示這兩人休年假次數之差的絕對值,求隨機變量
表示這兩人休年假次數之差的絕對值,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,且A={x||x-1|>2},B={x|x2-6x+8<0},則(UA)∩B等于( )
A. [-1,4) B. (2,3)
C. (2,3] D. (-1,4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品生產線上,一天內每隔60分鐘抽取一件產品,則該抽樣方法為①;某中學從30名機器人愛好者中抽取3人了解學習負擔情況,則該抽取方法為②,那么
A. ①是系統抽樣,②是簡單隨機抽樣 B. ①是分層抽樣,②是簡單隨機抽樣
C. ①是系統抽樣,②是分層抽樣 D. ①是分層抽樣,②是系統抽樣
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com