
【題目】如圖1,已知直角梯形ABCD中,![]() ,AB//DC,AB⊥AD,E為CD的中點,沿AE把△DAE折起到△PAE的位置(D折后變為P),使得PB=2,如圖2.
,AB//DC,AB⊥AD,E為CD的中點,沿AE把△DAE折起到△PAE的位置(D折后變為P),使得PB=2,如圖2.
(Ⅰ)求證:平面PAE⊥平面ABCE;
(Ⅱ)求點B到平面PCE的距離.

【答案】(1)見解析(2)![]()
【解析】試題分析:![]() 取
取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,
,![]() 為等腰直角三角形,證得
為等腰直角三角形,證得![]() ,
,![]() ,再由勾股定理證得
,再由勾股定理證得![]() ,即可證明
,即可證明 ![]() 利用等體積法
利用等體積法![]() ,即可求點
,即可求點![]() 到平面
到平面![]() 的距離
的距離
解析:(Ⅰ)如圖,取AE的中點O,連接PO,OB,BE.由于在平面圖形中,如題圖1,連接BD,BE,易知四邊形ABED為正方形, ∴在立體圖形中,△PAE,△BAE為等腰直角三角形,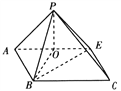
∴PO⊥AE,OB⊥AE,PO=OB=![]() ,
,
∵PB=2,∴![]() ,
,
∴PO⊥OB
又![]() ,∴平面PO⊥平面ABCE,
,∴平面PO⊥平面ABCE,
∵PO![]() 平面PAE,∴平面PAE⊥平面ABCD
平面PAE,∴平面PAE⊥平面ABCD
(Ⅱ)由(Ⅰ)可知,PO⊥AE,OB⊥AE,![]() ,故AE⊥平面POB.
,故AE⊥平面POB.
∵PB![]() 平面POB,∴AE⊥PB,又BC//AE,∴BC⊥PB.
平面POB,∴AE⊥PB,又BC//AE,∴BC⊥PB.
在Rt△PBC中,![]()
在△PEC中,PE=CE=2,
∴![]()
設點B到平面PCE的距離為d,由![]() ,
,
得![]()


科目:高中數學 來源: 題型:
【題目】二進制規定:每個二進制數由若干個0、1組成,且最高位數字必須為1.若在二進制中,![]() 是所有
是所有![]() 位二進制數構成的集合,對于
位二進制數構成的集合,對于![]() ,
,![]() ,
,![]() 表示
表示![]() 和
和![]() 對應位置上數字不同的位置個數.例如當
對應位置上數字不同的位置個數.例如當![]() ,
,![]() 時
時![]() ,當
,當![]() ,
,![]() 時
時![]() .
.
(1)令![]() ,求所有滿足
,求所有滿足![]() ,且
,且![]() 的
的![]() 的個數;
的個數;
(2)給定![]() ,對于集合
,對于集合![]() 中的所有
中的所有![]() ,求
,求![]() 的和.
的和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)在極坐標系下,設曲線![]() 與射線
與射線![]() 和射線
和射線![]() 分別交于
分別交于![]() ,
,![]() 兩點,求
兩點,求![]() 的面積;
的面積;
(2)在直角坐標系下,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 軸,
軸, ![]() 軸分別相交于點
軸分別相交于點![]() 和點
和點![]() ,且
,且![]() ,點
,點![]() 是點
是點![]() 關于
關于![]() 軸的對稱點,
軸的對稱點, ![]() 的延長線交橢圓于點
的延長線交橢圓于點![]() ,過點
,過點![]() 分別做
分別做![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() .
.
(1) 若橢圓![]() 的左、右焦點與其短軸的一個端點是正三角形的三個頂點,點
的左、右焦點與其短軸的一個端點是正三角形的三個頂點,點![]() 在橢圓
在橢圓![]() 上,求橢圓
上,求橢圓![]() 的方程;
的方程;
(2)當![]() 時,若點
時,若點![]() 平分線段
平分線段![]() ,求橢圓
,求橢圓![]() 的離心率.
的離心率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線a與平面![]() 所成角的為30o,直線b在平面
所成角的為30o,直線b在平面![]() 內,且與b異面,若直線a與直線b所成的角為
內,且與b異面,若直線a與直線b所成的角為![]() ,則( )
,則( )
A. 0<![]() ≤30 B. 0<
≤30 B. 0<![]() ≤90 C. 30≤
≤90 C. 30≤![]() ≤90 D. 30≤
≤90 D. 30≤![]() ≤180
≤180
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以原點為極點,
為參數),在以原點為極點, ![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的傾斜角;
的傾斜角;
(2)設點![]() ,直線
,直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() 為直角梯形,
為直角梯形,![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() ,
,![]() ,三棱錐
,三棱錐![]() 的體積為9.
的體積為9.

(1)求![]() 的值;
的值;
(2)過![]() 點的平面
點的平面![]() 平行于平面
平行于平面![]() ,
,![]() 與棱
與棱![]() ,
,![]() ,
,![]() ,
,![]() 分別相交于點
分別相交于點![]() ,求截面
,求截面![]() 的周長.
的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com