
【題目】設數列{an}的前n項和為Sn , 若 ![]() (n∈N*),則稱{an}是“緊密數列”;
(n∈N*),則稱{an}是“緊密數列”;
(1)若a1=1, ![]() ,a3=x,a4=4,求x的取值范圍;
,a3=x,a4=4,求x的取值范圍;
(2)若{an}為等差數列,首項a1 , 公差d,且0<d≤a1 , 判斷{an}是否為“緊密數列”;
(3)設數列{an}是公比為q的等比數列,若數列{an}與{Sn}都是“緊密數列”,求q的取值范圍.
【答案】
(1)解:由題意, ![]() 且
且 ![]() ,∴2≤x≤3,
,∴2≤x≤3,
∴x的取值范圍是[2,3];
(2)解:由題意,an=a1+(n﹣1)d,∴ ![]() ,
,
![]() 隨著n的增大而減小,所以當n=1時,
隨著n的增大而減小,所以當n=1時, ![]() 取得最大值,∴
取得最大值,∴ ![]() ≤2,
≤2,
∴{an}是“緊密數列”;
(3)解:由題意得,等比數列{an}的公比q
當q≠1時,所以an=a1qn﹣1,Sn= ![]() ,
, ![]() ,
,
因為數列{an}與{Sn}都是“緊密數列”,所以 ![]() ,
, ![]() ,解得
,解得 ![]() ,
,
當q=1時,an=a1,Sn=na1,則 ![]() =1,
=1, ![]() ,符合題意,
,符合題意,
∴q的取值范圍是 ![]() .
.
【解析】(1)由題意, ![]() 且
且 ![]() ,即可求出x的取值范圍;(2)由題意,an=a1+(n﹣1)d,
,即可求出x的取值范圍;(2)由題意,an=a1+(n﹣1)d, ![]() ,根據“緊密數列”的定義即可證明結論;(3)先設公比是q并判斷出q≠1,由等比數列的通項公式、前n項和公式化簡
,根據“緊密數列”的定義即可證明結論;(3)先設公比是q并判斷出q≠1,由等比數列的通項公式、前n項和公式化簡 ![]() ,根據“緊密數列”的定義列出不等式組,再求出公比q的取值范圍.
,根據“緊密數列”的定義列出不等式組,再求出公比q的取值范圍.


科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC﹣A1BlC1中,平面α與棱AB,AC,A1C1 , A1B1分別交于點E,F,G,H,且直線AA1∥平面α.有下列三個命題:①四邊形EFGH是平行四邊形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正確的命題有( )
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M過C(1,-1),D(-1,1)兩點,且圓心M在x+y-2=0上.
(1)求圓M的方程;
(2)設點P是直線3x+4y+8=0上的動點,PA,PB是圓M的兩條切線,A,B為切點,求四邊形PAMB面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐母線長為5,底面圓半徑長為4,點M是母線PA的中點,AB是底面圓的直徑,點C是弧AB的中點; 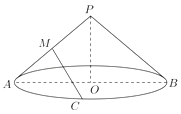
(1)求三棱錐P﹣ACO的體積;
(2)求異面直線MC與PO所成的角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】長方體ABCD-A1B1C1D1中,AA1=AB=2,AD=1,點E、F、G分別是DD1、AB、CC1的中點.求異面直線A1E與GF所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l1:x-2y+3=0與直線l2:2x+3y-8=0的交點為M,
(1)求過點M且到點P(0,4)的距離為2的直線l的方程;
(2)求過點M且與直線l3:x+3y+1=0平行的直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com