
【題目】下列說法錯誤的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
B.若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為真命題
均為真命題
C.命題“若![]() ,則
,則![]() ”的逆否命題是“若
”的逆否命題是“若![]() ,則
,則![]() |”
|”
D.若命題![]() ,使得
,使得![]() ,則
,則![]() ,恒有
,恒有![]()
科目:高中數學 來源: 題型:
【題目】如圖,在南北方向有一條公路,一半徑為100![]() 的圓形廣場(圓心為
的圓形廣場(圓心為![]() )與此公路所在直線
)與此公路所在直線![]() 相切于點
相切于點![]() ,點
,點![]() 為北半圓弧(弧
為北半圓弧(弧![]() )上的一點,過點
)上的一點,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,計劃在
,計劃在![]() 內(圖中陰影部分)進行綠化,設
內(圖中陰影部分)進行綠化,設![]() 的面積為
的面積為![]() (單位:
(單位:![]() ),
),
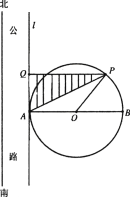
(1)設![]() ,將
,將![]() 表示為
表示為![]() 的函數;
的函數;
(2)確定點![]() 的位置,使綠化面積最大,并求出最大面積.
的位置,使綠化面積最大,并求出最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1),在平面五邊形![]() 中,已知四邊形
中,已知四邊形![]() 為正方形,
為正方形,![]() 為正三角形.沿著
為正三角形.沿著![]() 將四邊形
將四邊形![]() 折起得到四棱錐
折起得到四棱錐![]() ,使得平面
,使得平面![]() 平面
平面![]() ,設
,設![]() 在線段
在線段![]() 上且滿足
上且滿足![]() ,
,![]() 在線段
在線段![]() 上且滿足
上且滿足![]() ,
,![]() 為
為![]() 的重心,如圖(2).
的重心,如圖(2).
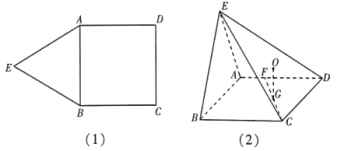
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市的公交公司為了方便市民出行,科學規劃車輛投放,在一個人員密集流動地段增設一個起點站,為了研究車輛發車間隔時間![]() 與乘客等候人數
與乘客等候人數![]() 之間的關系,經過調查得到如下數據:
之間的關系,經過調查得到如下數據:
間隔時間/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人數y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
調查小組先從這![]() 組數據中選取
組數據中選取![]() 組數據求線性回歸方程,再用剩下的
組數據求線性回歸方程,再用剩下的![]() 組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數
組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數
與實際等候人數![]() 的差,若差值的絕對值都不超過
的差,若差值的絕對值都不超過![]() ,則稱所求方程是“恰當回歸方程”.
,則稱所求方程是“恰當回歸方程”.
(1)從這![]() 組數據中隨機選取
組數據中隨機選取![]() 組數據后,求剩下的
組數據后,求剩下的![]() 組數據的間隔時間不相鄰的概率;
組數據的間隔時間不相鄰的概率;
(2)若選取的是后面![]() 組數據,求
組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判斷此方程是否是“恰當回歸方程”;
,并判斷此方程是否是“恰當回歸方程”;
(3)為了使等候的乘客不超過![]() 人,試用(2)中方程估計間隔時間最多可以設置為多少(精確到整數)分鐘.
人,試用(2)中方程估計間隔時間最多可以設置為多少(精確到整數)分鐘.
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 為
為![]() 的中點,平面
的中點,平面![]() 平面
平面![]() .
.
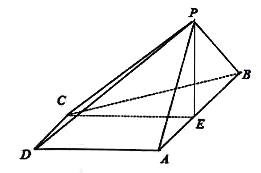
(1)求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為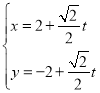 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設點![]() ,
,![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(Ⅰ)求直線![]() 與曲線
與曲線![]() 公共點的極坐標;
公共點的極坐標;
(Ⅱ)設過點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 與
與![]() 的交點
的交點![]() 恰好是
恰好是![]() 中點,又
中點,又![]() ,
,![]() .
.
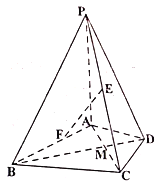
(1)求證:![]() ;
;
(2)設![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,若直線
上,若直線![]() 平面
平面![]() ,求
,求![]() 的長;
的長;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com