
甲、乙兩名運動員參加“選拔測試賽”,在相同條件下,兩人5次測試的成績(單位:分)記錄如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用莖葉圖表示這兩組數據;.
(2)現要從中選派一名運動員參加比賽,你認為選派誰參賽更好?說明理由(不用計算);
(3)若將頻率視為概率,對運動員甲在今后三次測試成績進行預測,記這三次成績高于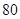 分的次數為
分的次數為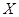 ,求
,求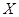 的分布列和數學期望
的分布列和數學期望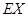 ..
..
(1)莖葉圖見解析;(2)乙;(3).
解析試題分析:(1)莖葉圖是將數組中的數按位數進行比較,將數的大小基本不變或變化不大的位作為一個主干(莖),將變化大的位的數作為分枝(葉),列在主干的后面,這樣就可以清楚地看到每個主干后面的幾個數,每個數具體是多少。 在制作莖葉圖時,重復出現的數據要重復記錄,不能遺漏,特別是“葉”部分,同一數據出現幾次,就要在圖中體現幾次;(2)可計算出兩人的平均成績,方差(以說明他的穩定性),最高成績等數據,然后比較得出結論;(3)記“甲成績高于80分”為事件 ,則
,則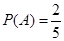 ,甲在今后三次測試,這三次成績高于
,甲在今后三次測試,這三次成績高于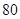 分的次數為
分的次數為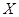 符合二項分布
符合二項分布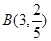 ,其中
,其中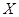 取值依次為
取值依次為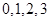 ,根據公式可求出相應的概率,從而寫出其概率分布列,再根據期望公式計算出數學期望.
,根據公式可求出相應的概率,從而寫出其概率分布列,再根據期望公式計算出數學期望.
(1)莖葉圖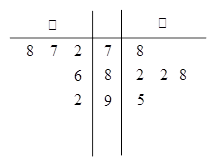 3分
3分
(2)由圖可知,乙的平均成績大于甲的平均成績,且乙的方差小于甲的方差,且乙的最高分高于甲的最高分,因此應選派乙參賽更好. 6分
(3)記甲“高于80分”為事件A,
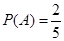

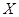
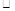

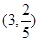 ,
,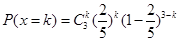 8分
8分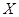 的可能取值為
的可能取值為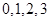 .
.
分布列為: 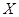
0 1 2 3 
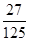
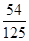
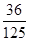
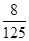
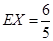 13分
13分
考點:(1)莖葉圖;(2)樣本數據的特征;(3)隨機變量的概率分布列與數學期望.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:解答題
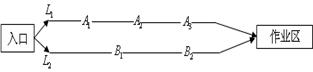
某煤礦發生透水事故時,作業區有若干人員被困.救援隊從入口進入之后有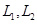 兩條巷道通往作業區(如下圖),
兩條巷道通往作業區(如下圖),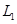 巷道有
巷道有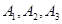 三個易堵塞點,各點被堵塞的概率都是
三個易堵塞點,各點被堵塞的概率都是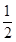 ;
;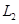 巷道有
巷道有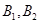 兩個易堵塞點,被堵塞的概率分別為
兩個易堵塞點,被堵塞的概率分別為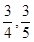 .
.
(1)求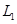 巷道中,三個易堵塞點最多有一個被堵塞的概率;
巷道中,三個易堵塞點最多有一個被堵塞的概率;
(2)若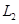 巷道中堵塞點個數為
巷道中堵塞點個數為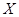 ,求
,求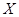 的分布列及數學期望
的分布列及數學期望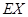 ,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
小波以游戲方式決定是去打球、唱歌還是去下棋。游戲規則為:以O為起點,再從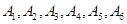 (如圖)這六個點中任取兩點分別為終點得到兩個向量,記這兩個向量的數量積為
(如圖)這六個點中任取兩點分別為終點得到兩個向量,記這兩個向量的數量積為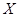 ,若
,若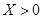 就去打球,若
就去打球,若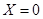 就去唱歌,若
就去唱歌,若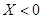 就去下棋。
就去下棋。
(1)寫出數量積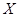 的所有可能值;
的所有可能值;
(2)分別求小波去下棋的概率和不去唱歌的概率。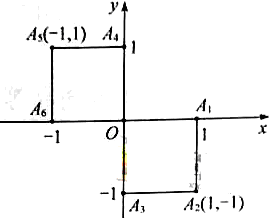
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,A地到火車站共有兩條路徑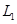 和
和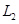 ,據統計,通過兩條路徑所用的時間互不影響,所用時間落在個時間段內的頻率如下表:
,據統計,通過兩條路徑所用的時間互不影響,所用時間落在個時間段內的頻率如下表: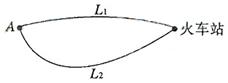
| 時間(分鐘) | 10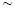 20 20 | 20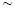 30 30 | 30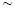 40 40 | 40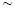 50 50 | 50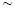 60 60 |
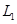 的頻率 的頻率 | 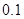 | 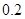 | 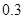 | 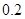 | 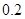 |
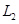 的頻率 的頻率 | 0 | 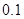 | 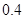 | 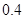 | 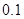 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個均勻的正四面體面上分別涂有1,2,3,4四個數字,現隨機投擲兩次,正四面體面朝下的數字分別為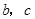 .
.
(1)記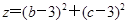 ,求
,求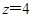 的概率;
的概率;
(2)若方程 至少有一根
至少有一根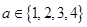 ,就稱該方程為“漂亮方程”,求方程為“漂亮方程”的概率.
,就稱該方程為“漂亮方程”,求方程為“漂亮方程”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
先后拋擲一枚骰子,得到的點數分別記為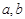 ,按以下程序進行運算:
,按以下程序進行運算:
(1)若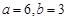 ,求程序運行后計算機輸出的y的值;
,求程序運行后計算機輸出的y的值;
(2)若“輸出y的值是3”為事件A,求事件A發生的概率.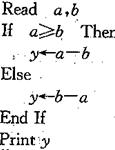
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一批產品需要進行質量檢驗,檢驗方案是:先從這批產品中任取4件作檢驗,這4件產品中優質品的件數記為n.如果n=3,再從這批產品中任取4件作檢驗,若都為優質品,則這批產品通過檢驗;如果n=4,再從這批產品中任取1件作檢驗,若為優質品,則這批產品通過檢驗;其他情況下,這批產品都不能通過檢驗.
假設這批產品的優質品率為50%,即取出的產品是優質品的概率都為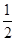 ,且各件產品是否為優質品相互獨立.
,且各件產品是否為優質品相互獨立.
(1)求這批產品通過檢驗的概率;
(2)已知每件產品檢驗費用為100元,凡抽取的每件產品都需要檢驗,對這批產品作質量檢驗所需的費用記為X(單位:元),求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
圖是某市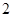 月
月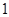 日至
日至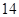 日的空氣質量指數趨勢圖,空氣質量指數(
日的空氣質量指數趨勢圖,空氣質量指數(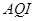 )小于
)小于 表示空氣質量優良,空氣質量指數大于
表示空氣質量優良,空氣質量指數大于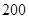 表示空氣重度污染,某人隨機選擇
表示空氣重度污染,某人隨機選擇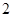 月
月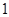 日至
日至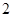 月
月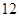 日中的某一天到達該市,并停留
日中的某一天到達該市,并停留 天.
天.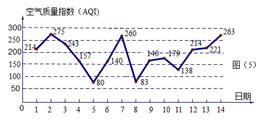
(1)求此人到達當日空氣質量優良的概率;
(2)求此人停留期間至多有1天空氣重度污染的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工藝廠開發一種新工藝品,頭兩天試制中,該廠要求每位師傅每天制作10件,該廠質檢部每天從每位師傅制作的10件產品中隨機抽取4件進行檢查,若發現有次品,則當天該師傅的產品不能通過.已知李師傅第一天、第二天制作的工藝品中分別有2件、1件次品.
(1)求兩天中李師傅的產品全部通過檢查的概率;
(2)若廠內對師傅們制作的工藝品采用記分制,兩天全不通過檢查得0分,通過1天、2天分別得1分、2分,求李師傅在這兩天內得分的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com