
【題目】某省高考改革新方案,不分文理科,高考成績實行“![]() ”的構成模式,第一個“3”是語文、數學、外語,每門滿分150分,第二個“3”由考生在思想政治、歷史、地理、物理、化學、生物6個科目中自主選擇其中3個科目參加等級性考試,每門滿分100分,高考錄取成績卷面總分滿分750分.為了調查學生對物理、化學、生物的選考情況,將“某市某一屆學生在物理、化學、生物三個科目中至少選考一科的學生”記作學生群體
”的構成模式,第一個“3”是語文、數學、外語,每門滿分150分,第二個“3”由考生在思想政治、歷史、地理、物理、化學、生物6個科目中自主選擇其中3個科目參加等級性考試,每門滿分100分,高考錄取成績卷面總分滿分750分.為了調查學生對物理、化學、生物的選考情況,將“某市某一屆學生在物理、化學、生物三個科目中至少選考一科的學生”記作學生群體![]() ,從學生群體
,從學生群體![]() 中隨機抽取了50名學生進行調查,他們選考物理,化學,生物的科目數及人數統計如下表:
中隨機抽取了50名學生進行調查,他們選考物理,化學,生物的科目數及人數統計如下表:

(I)從所調查的50名學生中任選2名,求他們選考物理、化學、生物科目數量不相等的概率;
(II)從所調查的50名學生中任選2名,記![]() 表示這2名學生選考物理、化學、生物的科目數量之差的絕對值,求隨機變量
表示這2名學生選考物理、化學、生物的科目數量之差的絕對值,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(III)將頻率視為概率,現從學生群體![]() 中隨機抽取4名學生,記其中恰好選考物理、化學、生物中的兩科目的學生數記作
中隨機抽取4名學生,記其中恰好選考物理、化學、生物中的兩科目的學生數記作![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
【答案】(Ⅰ)![]() ; (Ⅱ)見解析; (Ⅲ)
; (Ⅱ)見解析; (Ⅲ)![]() .
.
【解析】試題分析:(Ⅰ)設“所選取的2名學生選考物理、化學、生物科目數量相等”為事件的概率,從而得到選考物理、化學、生物科目數量不相等的概率;
(Ⅱ)由題意得到隨機變量的取值,計算其概率,列出分布列,根據公式求解數學期望.
(Ⅲ)由題意得所調查的學生中物理、化學、生物選考兩科目的學生的人數,得到相應的概率,即可求解“![]() ”的概率.
”的概率.
試題解析:(Ⅰ)記“所選取的2名學生選考物理、化學、生物科目數量相等”為事件A
則![]()
所以他們選考物理、化學、生物科目數量不相等的概率為
![]()
(Ⅱ)由題意可知X的可能取值分別為0,1,2
![]() ,
, ![]()
![]()
從而X的分布列為
X | 0 | 1 | 2 |
P |
|
|
|
![]()
(Ⅲ)所調查的50名學生中物理、化學、生物選考兩科目的學生有25名
相應的概率為![]() ,所以
,所以![]()
![]()
所以事件“![]() ”的概率為
”的概率為
![]()


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,左、右頂點分別為
,左、右頂點分別為![]() 為直徑的圓O過橢圓E的上頂點D,直線DB與圓O相交得到的弦長為
為直徑的圓O過橢圓E的上頂點D,直線DB與圓O相交得到的弦長為![]() .設點
.設點![]() ,連接PA交橢圓于點C.
,連接PA交橢圓于點C.
(I)求橢圓E的方程;
(II)若三角形ABC的面積不大于四邊形OBPC的面積,求t的最小值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】種子發芽率與晝夜溫差有關.某研究性學習小組對此進行研究,他們分別記錄了3月12日至3月16日的晝夜溫差與每天100顆某種種子浸泡后的發芽數,如下表:

(I)從3月12日至3月16日中任選2天,記發芽的種子數分別為c,d,求事件“c,d均不小于25”的概率;
(II)請根據3月13日至3月15日的三組數據,求出y關于x的線性回歸方程![]() ;
;
(III)若由線性回歸方程得到的估計數據與實際數據誤差均不超過2顆,則認為回歸方程是可靠的,試用3月12日與16日的兩組數據檢驗,(II)中的回歸方程是否可靠?
查看答案和解析>>
科目:高中數學 來源: 題型:
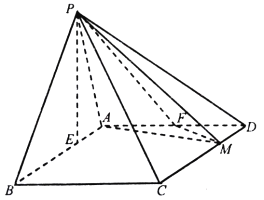
【題目】在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 點在底面
點在底面![]() 內的射影
內的射影![]() 在線段
在線段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(Ⅰ)當![]() 時,證明:平面
時,證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)當平面![]() 與平面
與平面![]() 所成的二面角的正弦值為
所成的二面角的正弦值為![]() 時,求四棱錐
時,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com