已知函數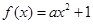
（
），
．
（Ⅰ）若曲線
與在它們的交點
處具有公共切線，求
的值；
（Ⅱ）當
時，求函數
在區間
上的最大值．
科目：高中數學 來源： 題型：解答題
某單位設計的兩種密封玻璃窗如圖所示：圖1是單層玻璃，厚度為8 mm；圖2是雙層中空玻璃，厚度均為4 mm，中間留有厚度為
的空氣隔層．根據熱傳導知識，對于厚度為
的均勻介質，兩側的溫度差為
，單位時間內，在單位面積上通過的熱量
，其中
為熱傳導系數．假定單位時間內，在單位面積上通過每一層玻璃及空氣隔層的熱量相等．（注：玻璃的熱傳導系數為
，空氣的熱傳導系數為
．）
（1）設室內，室外溫度均分別為
，
，內層玻璃外側溫度為
，外層玻璃內側溫度為
，且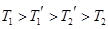
．試分別求出單層玻璃和雙層中空玻璃單位時間內，在單位面積上通過的熱量（結果用，及表示）；
（2）為使雙層中空玻璃單位時間內，在單位面積上通過的熱量只有單層玻璃的4%，應如何設計的大小？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
為了在夏季降溫和冬季供暖時減少能源損耗，房屋的房頂和外墻需要建造隔熱層，某幢建筑物要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元，該建筑物每年的能源消耗費用為C（單位：萬元）與隔熱層厚度x（單位：cm）滿足關系：C（x）=
（0
x10），若不建隔熱層，每年能源消耗費用為8萬元。設f（x）為隔熱層建造費用與20年的能源消耗費用之和。
(1)求k的值及f(x)的表達式；
(2)隔熱層修建多厚時，總費用f（x）達到最小，并求最小值。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
作為紹興市2013年5.1勞動節系列活動之一的花卉展在鏡湖濕地公園舉行．現有一占地1800平方米的矩形地塊，中間三個矩形設計為花圃（如圖），種植有不同品種的觀賞花卉，周圍則均是寬為1米的賞花小徑，設花圃占地面積為
平方米，矩形一邊的長為
米(如圖所示)
（1）試將表示為的函數;
（2）問應該如何設計矩形地塊的邊長，使花圃占地面積取得最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
若二次函數f(x)＝ax2＋bx＋c(a≠0)滿足f(x＋1)－f(x)＝2x，且f(0)＝1.
(1)求f(x)的解析式；
(2)若在區間[－1,1]上，不等式f(x)>2x＋m恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某租賃公司擁有汽車100輛，當每輛車的月租金為3000元時，可全部租出。當每輛車的月租金每增加50元時，未租出的車將會增加一輛。租出的車每輛每月需要維護費150元，未租出的車每輛每月需要維護費50元。
（1）當每輛車的月租金定為3600元時，能租出多少輛車？
（2）當每輛車的月租金定為多少元時，租賃公司的月收益最大？最大月收益是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某工廠生產一種產品的原材料費為每件40元，若用x表示該廠生產這種產品的總件數，則電力與機器保養等費用為每件0．05x元，又該廠職工工資固定支出12500元。
（1）把每件產品的成本費P（x）（元）表示成產品件數x的函數，并求每件產品的最低成本費；
（2）如果該廠生產的這種產品的數量x不超過3000件，且產品能全部銷售，根據市場調查：每件產品的銷售價Q（x）與產品件數x有如下關系：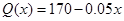
，試問生產多少件產品，總利潤最高？（總利潤=總銷售額-總的成本）
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
一邊長為
的正方形鐵片，鐵片的四角截去四個邊長均為
的小正方形，然后做成一個無蓋方盒。
（1）試把方盒的容積
表示為的函數；
（2）多大時，方盒的容積最大？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
時，
時，
在
，
上單調遞增，在
上單調遞減
（1）當
即
即
時,求不等式
的解集; (2)若
的解集包含
,求
的取值范圍.