(本小題8分)
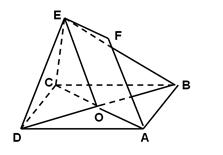
如圖,正方形ABCD和四邊形ACEF所在的平面互相垂直. EF//AC,AB=
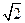
,CE=EF=1,
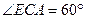
.
(1)求證:AF//平面BDE;
(2)求異面直線AB與DE所成角的余弦值.
(1)略
(2)
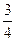
(1)證明:
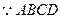
是正方形,且AB=
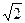
,

AO=1,又
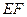
//
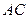
,EF=1,

EFAO為平行四邊形,則
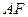
//
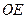
,而
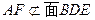
,
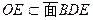
,

AF//面BDE ………………………………………………(3分)
(2)解:
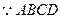
是正方形,

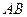
//
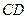

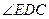
為異面直線AB與DE所成的角或其補角 …………………………(2分)
又
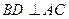
,又面ABCD
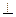
面ACEF,且面ABCD
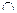
面ACEF=AC

BD
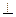
面ACEF,又
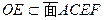
,

BD
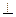
OE.
而由EC=1,OC=OA=1,
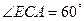

OE=1,又OD=1,則ED=
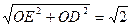
又CD=
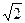
,CE="1,"

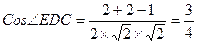

異面直線AB與DE所成的角的余弦值為
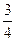
……………………………………(3分)
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(12分)如圖所示,正方形
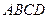
和矩形
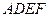
所在平面相互垂直,
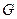
是
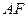
的中點.
(I)求證:
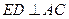
;
(Ⅱ)若直線

與平面
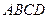
成45
o角,
求異面直線
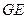
與
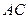
所成角的余弦值.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在三棱錐
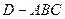
中,已知△
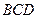
是正三角形,
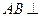
平面
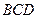
,
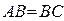 ,
,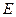
為
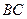
的中點,
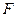
在棱
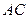
上,且
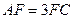
,
(1)求證:
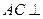
平面
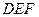
;
(2)求平面
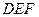
與平面
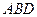
所成的銳二面角的余弦值;
(3)若
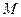
為
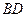
的中點,問
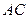
上是否存在一點
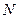
,使
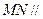
平面
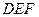
?若存在,說明點
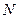
的位置;若不存在,試說明理由.
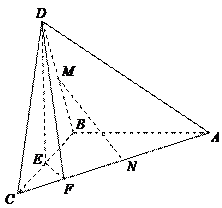
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分14分)如圖,三棱錐A—BPC中,AP⊥PC,AC⊥BC,M為AB中點,D為PB中點,且△PMB為正三角形。
(Ⅰ)求證:DM//平面APC;
(Ⅱ)求證:BC⊥平面APC;
(Ⅲ)若BC=4,AB=20,求三棱錐D—BCM的體積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
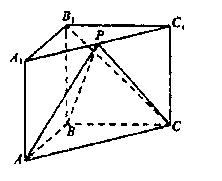
如圖,在直三棱柱ABC—A
1B
1C
1中,AB⊥BC,P為A
1C
1的中點,AB=BC=kPA。
(I)當(dāng)k=1時,求證PA⊥B
1C;
(II)當(dāng)k為何值時,直線PA與平面BB
1C
1C所成的角的正弦值為
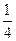
,并求此時二面角A—PC—B的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知三棱錐

的四個頂點均在半徑為

的球面上,且滿足

,

,

,則三棱錐

的側(cè)面積的最大值為
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
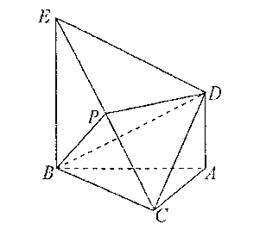
如圖,
為正三角形,
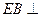
平面ABC,AD//BE,且BE=AB+2AD,P是EC的中點。
求證:(1)PD//平面ABC;
(2)EC
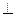
平面PBD。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在正方體上任意選擇4個頂點,它們可能是如下幾何體的4個頂點,請寫出所有符合題意的幾何體的序號 .
①矩形 ②不是矩形的平行四邊形
③有三個面為等腰直角三角形,另一個面為等邊三角形的四面體
④每個面都是等邊三角形的四面體
⑤每個面都是直角三角形的四面體
查看答案和解析>>

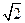 ,CE=EF=1,
,CE=EF=1,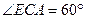 .
.
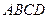 和矩形
和矩形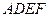 所在平面相互垂直,
所在平面相互垂直,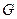 是
是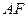 的中點.
的中點.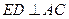 ;
; 與平面
與平面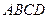 成45o角,
成45o角,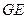 與
與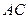 所成角的余弦值.
所成角的余弦值.
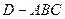 中,已知△
中,已知△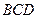 是正三角形,
是正三角形,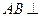 平面
平面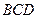 ,
,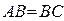 ,
,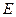 為
為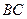 的中點,
的中點,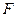 在棱
在棱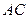 上,且
上,且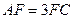 ,
, 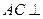 平面
平面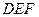 ;
;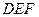 與平面
與平面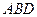 所成的銳二面角的余弦值;
所成的銳二面角的余弦值;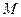 為
為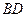 的中點,問
的中點,問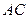 上是否存在一點
上是否存在一點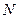 ,使
,使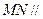 平面
平面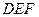 ?若存在,說明點
?若存在,說明點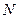 的位置;若不存在,試說明理由.
的位置;若不存在,試說明理由.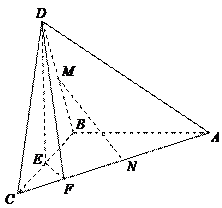
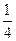 ,并求此時二面角A—PC—B的余弦值。
,并求此時二面角A—PC—B的余弦值。
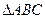 為正三角形,
為正三角形,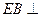 平面ABC,AD//BE,且BE=AB+2AD,P是EC的中點。
平面ABC,AD//BE,且BE=AB+2AD,P是EC的中點。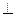 平面PBD。
平面PBD。