
【題目】為了解甲、乙兩個快遞公司的工作狀況,假設同一個公司快遞員的工作狀況基本相同,現從甲、乙兩公司各隨機抽取一名快遞員,并從兩人某月(30天)的快遞件數記錄結果中隨機抽取10天的數據,制表如圖:

每名快遞員完成一件貨物投遞可獲得的勞務費情況如下:甲公司規定每件4.5元;乙公司規定每天35件以內(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根據表中數據寫出甲公司員工A在這10天投遞的快遞件數的平均數和眾數;
(2)為了解乙公司員工B的每天所得勞務費的情況,從這10天中隨機抽取1天,他所得的勞務費記為X(單位:元),求X的分布列和數學期望;
(3)根據表中數據估算兩公司的每位員工在該月所得的勞務費.
【答案】(1)平均數為![]() ,眾數為33;(2)詳見解析;(3)甲公司被抽取員工該月收入
,眾數為33;(2)詳見解析;(3)甲公司被抽取員工該月收入![]() 元,乙公司被抽取員工該月收入
元,乙公司被抽取員工該月收入![]() 元.
元.
【解析】
(1)直接利用莖葉圖中數據求甲公司員工A投遞快遞件數的平均數和眾數.
(2)由題意能求出X的可能取值為136,147,154,189,203,分別求出相對應的概率,由此能求出X的分布列和數學期望.
(3)利用(2)的結果能估算算兩公司的每位員工在該月所得的勞務費.
(1)甲公司員工A投遞快遞件數的平均數為:
![]() ,
,
眾數為33.
(2)設a為乙公司員工B投遞件數,則
當![]() 時,
時,![]() 元,
元,
當![]() 時,
時,![]() 元,
元,
![]() X的可能取值為136,147,154,189,203,
X的可能取值為136,147,154,189,203,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
X的分布列為:
X | 136 | 147 | 154 | 189 | 203 |
P |
|
|
|
|
|
![]() (元).
(元).
(3)根據圖中數據,由(2)可估算:
甲公司被抽取員工該月收入![]() 元,
元,
乙公司被抽取員工該月收入![]() 元.
元.


科目:高中數學 來源: 題型:
【題目】如圖,已知矩形ABCD中,![]() ,
,![]() ,M是以CD為直徑的半圓周上的任意一點(與C,D均不重合),且平面
,M是以CD為直徑的半圓周上的任意一點(與C,D均不重合),且平面![]() 平面ABCD.
平面ABCD.
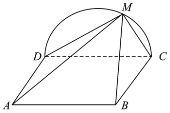
(1)求證:平面![]() 平面BCM;
平面BCM;
(2)當四棱錐![]() 的體積最大時,求AM與CD所成的角.
的體積最大時,求AM與CD所成的角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數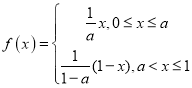 ,其中
,其中![]() 為常數且
為常數且![]() .新定義:若
.新定義:若![]() 滿足
滿足![]() ,但
,但![]() ,則稱
,則稱![]() 為
為![]() 的回旋點.
的回旋點.
(1)當![]() 時,分別求
時,分別求![]() 和
和![]() 的值;
的值;
(2)當![]() 時,求函數
時,求函數![]() 的解析式,并求出
的解析式,并求出![]() 回旋點;
回旋點;
(3)證明函數![]() 在
在![]() 有且僅有兩個回旋點,并求出回旋點
有且僅有兩個回旋點,并求出回旋點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個圓內有6000個點,其中任三點都不共線;①能否把這個圓分成2000塊,使每塊恰含有三個點,如何分?②若每塊中三點滿足:兩兩間的距離皆為整數且不超過9,則以每塊中的三點為頂點作三角形,這些三角形中大小完全一樣的三角形至少有多少個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 為等腰梯形,
為等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 分別是
分別是![]()
![]()
![]() 的中點.
的中點.
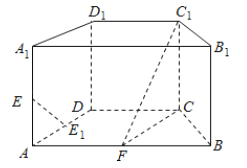
(1)證明:直線![]() 平面
平面![]() ;
;
(2)求直線![]() 與面
與面![]() 所成角的大小;
所成角的大小;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】探月工程“嫦娥四號”探測器于2018年12月8日成功發射,實現了人類首次月球背面軟著陸.以嫦娥四號為任務圓滿成功為標志,我國探月工程四期和深空探測工程全面拉開序幕.根據部署,我國探月工程到2020年前將實現“繞、落、回”三步走目標.為了實現目標,各科研團隊進行積極的備戰工作.某科研團隊現正準備攻克甲、乙、丙三項新技術,甲、乙、丙三項新技術獨立被攻克的概率分別為![]() ,若甲、乙、丙三項新技術被攻克,分別可獲得科研經費
,若甲、乙、丙三項新技術被攻克,分別可獲得科研經費![]() 萬,
萬,![]() 萬,
萬,![]() 萬.若其中某項新技術未被攻克,則該項新技術沒有對應的科研經費.
萬.若其中某項新技術未被攻克,則該項新技術沒有對應的科研經費.
(1)求該科研團隊獲得![]() 萬科研經費的概率;
萬科研經費的概率;
(2)記該科研團隊獲得的科研經費為隨機變量![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】楊輝三角是二項式系數在三角形中的一種排列,在歐洲這個表叫做帕斯卡三角形,帕斯卡是在1654年發現這一規律的,我國南宋數學家楊輝在1261年所著的《詳解九章算法》一書中出現了如圖所示的表,這是我國數學史上的一次偉大成就,如圖所示,在“楊輝三角”中去除所有為1的項,依次構成數列,2,3,3,4,6,4,5 ,10 ,10,5,……,則此數列的前119項的和為__________.(參考數據:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
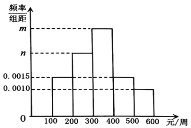
【題目】某網購平臺為了解某市居民在該平臺的消費情況,從該市使用其平臺且每周平均消費額超過100元的人員中隨機抽取了100名,并繪制右圖所示頻率分布直方圖,已知中間三組的人數可構成等差數列.
(1)求![]() 的值;
的值;
(2)分析人員對抽取對象每周的消費金額y與年齡x進一步分析,發現他們線性相關,得到回歸方程![]() .已知100名使用者的平均年齡為38歲,試判斷一名年齡為22歲的年輕人每周的平均消費金額為多少.(同一組數據用該區間的中點值代替)
.已知100名使用者的平均年齡為38歲,試判斷一名年齡為22歲的年輕人每周的平均消費金額為多少.(同一組數據用該區間的中點值代替)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com