
 •
• 的最大值 .
的最大值 . 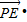
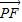 =4cos∠EPF,當∠EMF最大時,
=4cos∠EPF,當∠EMF最大時,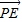 •
•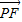 的值最大.由于當PM和直線3x+4y+8=0垂直時,∠EMF最大,此時,求得PM的值,即可求得cos∠PMF,利用二倍角
的值最大.由于當PM和直線3x+4y+8=0垂直時,∠EMF最大,此時,求得PM的值,即可求得cos∠PMF,利用二倍角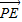 •
•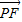 的值最大.
的值最大.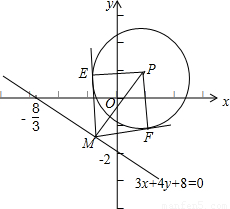 解:由題意可得
解:由題意可得 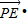
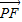 =2×2×cos∠EPF=4cos∠EPF,圓心P(1,1),故要使
=2×2×cos∠EPF=4cos∠EPF,圓心P(1,1),故要使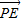 •
•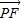 的值最大,只有∠EPF 最小.
的值最大,只有∠EPF 最小.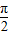 可得四邊形MEPF是圓內接四邊形,故∠EPF+∠EMF=π,故當∠EMF最大時,
可得四邊形MEPF是圓內接四邊形,故∠EPF+∠EMF=π,故當∠EMF最大時,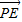 •
•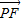 的值最大.
的值最大.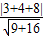 =3.
=3.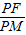 =
= ,cos∠EPF=cos(2∠MPF)=2cos2∠MPF-1=
,cos∠EPF=cos(2∠MPF)=2cos2∠MPF-1= -1=-
-1=- ,
,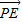 •
•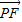 的值最大為 4cos∠EPF=4×(-
的值最大為 4cos∠EPF=4×(- )=-
)=- ,
, .
.

科目:高中數學 來源: 題型:
| PE |
| PF |
| 4 |
| 9 |
| 4 |
| 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
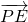 •
• 的最大值________.
的最大值________.查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省無錫市華士高級中學、成化高級中學高二(上)期中數學試卷(解析版) 題型:填空題
 •
• 的最大值 .
的最大值 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com