
【題目】已知橢圓C:![]() 1(a>b>0)的離心率e
1(a>b>0)的離心率e![]() ,且點P(
,且點P(![]() ,1)在橢圓C上.
,1)在橢圓C上.
(1)求橢圓C的方程;
(2)若橢圓C的左焦點為F,右頂點為A,點M(s,t)(t>0)是橢圓C上的動點,直線AM與y軸交于點D,點E是y軸上一點,EF⊥DF,EA與橢圓C交于點G,若△AMG的面積為2![]() ,求直線AM的方程.
,求直線AM的方程.
【答案】(1)![]() (2)x
(2)x![]() y﹣2=0
y﹣2=0
【解析】
(1)利用離心率和橢圓經過的點建立方程組,可以求解方程;
(2)設出直線方程,聯立方程組,結合三角形的面積為2![]() 可得直線斜率,從而可得方程.
可得直線斜率,從而可得方程.
(1)由題意得e![]() ,
,![]() ,a2=b2+c2,解得:a2=4,b2=2,
,a2=b2+c2,解得:a2=4,b2=2,
所以橢圓的方程:![]() .
.
(2)由(1)得左焦點F(![]() ,0),A(2,0),設直線AM:y=k(x﹣2),由題意得D(0,﹣2k),∴kDF
,0),A(2,0),設直線AM:y=k(x﹣2),由題意得D(0,﹣2k),∴kDF![]() k,
k,
∵EF⊥DF,∴kEF![]() ,∴直線EF的方程:x
,∴直線EF的方程:x![]() ,
,
令x=0,則y![]() ,所以點E(0,
,所以點E(0,![]() ),所以kEA
),所以kEA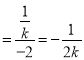 ,
,
所以直線EA:x=﹣2ky+2,聯立與橢圓的方程整理得:∴y![]() ,x
,x![]() ,所以點G(
,所以點G(![]() ,
,![]() );
);
聯立直線AM與橢圓的方程整理得:(1+2k2)x2﹣8k2x+8k2﹣4=0,解得:x1=2,x2![]() ,∴y2
,∴y2![]() ,所以點M(
,所以點M(![]() ,
,![]() ),
),
所以點M,G關于原點對稱,即直線MG過原點,
∴S△AMG![]() 2|yM|
2|yM|![]() ,由題意得:
,由題意得:![]() 2
2![]() ,解得:k
,解得:k![]() ,
,
由點M(s,t)(t>0)得,k![]() ,所以直線AM為:y
,所以直線AM為:y![]() (x﹣2),
(x﹣2),
即直線AM:x![]() y﹣2=0.
y﹣2=0.


科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,四邊形ABCD是菱形,AC,BD相交于點O,EF∥AB,EF![]() AB,平面BCF⊥平面ABCD,BF=CF,G為BC的中點,求證:
AB,平面BCF⊥平面ABCD,BF=CF,G為BC的中點,求證:

(1)OG∥平面ABFE;
(2)AC⊥平面BDE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數h(x)是定義在(﹣2,2)上,滿足h(﹣x)=﹣h(x),且x∈(0,2)時,h(x)=﹣2x,當x∈(﹣2,0)時,不等式[h(x)+2]2>h(x)m﹣1恒成立,則實數m的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() ),其中離心率
),其中離心率![]() ,點
,點![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 為橢圓的左右焦點,若
為橢圓的左右焦點,若![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 的上頂點,若
的上頂點,若![]() ,試問直線
,試問直線![]() 是否經過定點,若經過定點,求出定點坐標,否則說明理由.
是否經過定點,若經過定點,求出定點坐標,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體ABCDEF滿足:正方形ABCD與正三角形FBC所在的兩個平面互相垂直,FB∥AE且FB=2EA.
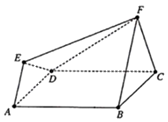
(1)證明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是R上的偶函數,對于
是R上的偶函數,對于![]() 都有
都有![]() 成立,且
成立,且![]() ,當
,當![]() ,且
,且![]() 時,都有
時,都有![]() .則給出下列命題:
.則給出下列命題:
①![]() ;
;
②函數![]() 圖象的一條對稱軸為
圖象的一條對稱軸為![]() ;
;
③函數![]() 在[﹣9,﹣6]上為減函數;④方程
在[﹣9,﹣6]上為減函數;④方程![]() 在[﹣9,9]上有4個根;
在[﹣9,9]上有4個根;
其中正確的命題序號是___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函數f(x)的定義域;
(2)討論函數f(x)的奇偶性;
(3)求a的取值范圍,使f(x)>0在定義域上恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為零的等差數列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比數列,
成等比數列,
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 滿足
滿足![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,若不等式
,若不等式![]() 對一切
對一切![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
(3)設數列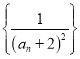 的前n項和為
的前n項和為![]() ,求證:對任意正整數n,都有
,求證:對任意正整數n,都有![]() 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com