分析:根據題中所給的程序框圖,可知該程序的功能是計算一個分段函數,將分段函數的解析式表示出來,進行分類求解不等式
f(x)≥-x+2的解集,從而得到答案.
解答:解:根據程序框圖可知,該程序的功能為計算f(x)=
| | 2x+1,x≤1 | | x+3,1<x≤2 | | 8-2x,x>2 |
| |
,
∵不等式
f(x)≥-x+2,
①當x≤1時,f(x)=2
x+1,
故不等式即為2
x+1≥
-x+2,即2
x+1+
x-2≥0,
令g(x)=2
x+1+
x-2,則g′(x)=2
x+1+
>0恒成立,
∴g(x)=2
x+1+
x-2在(-∞,1]上單調遞增,
∵g(0)=0,
又∵g(x)≥0,
∴x≥0,且x≤1,即0≤x≤1,
故不等式
f(x)≥-x+2的解集為{x|0≤x≤1};
②當1<x≤2時,f(x)=x+3,
故不等式即為x+3≥
-x+2,
解得x≤-
,
又∵1<x≤2,
故不等式
f(x)≥-x+2的解集為∅;
③當x>2時,f(x)=8-2x,
故不等式即為8-2x≥
-x+2,
解得x≤4,
故不等式
f(x)≥-x+2的解集為{x|2<x≤4}.
綜合①②③可得,不等式
f(x)≥-x+2的解集為[0,4].
故答案為:[0,4].
點評:本題考查了程序框圖,分段函數問題.程序框圖中對應的知識點是條件結構,其中正確理解各變量的含義并根據程序功能的需要合理的分析是解答的關鍵.考查了分段函數的解不等式,該題是分段函數故需討論用哪段解析式,同時考查了利用函數單調性解不等式.屬于基礎題.

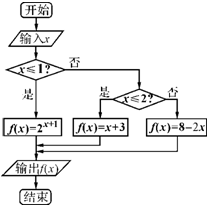 已知x∈R,根據右圖所示的程序框圖,則不等式f(x)≥-
已知x∈R,根據右圖所示的程序框圖,則不等式f(x)≥-

 名校課堂系列答案
名校課堂系列答案