
【題目】若一個四棱錐底面為正方形,頂點在底面的射影為正方形的中心,且該四棱錐的體積為9,當其外接球表面積最小時,它的高為( )
A.3
B.2 ![]()
C.2 ![]()
D.3 ![]()
【答案】A
【解析】解:設底面邊長AB=a,棱錐的高SM=h, ∵V棱錐S﹣ABCD= ![]() a2h=9,
a2h=9,
∴a2= ![]() ,
,
∵正四棱錐內接于球O,
∴O在直線SM上,設球O半徑為R,
(i)若O在線段SM上,如圖一,則OM=SM﹣SO=h﹣R,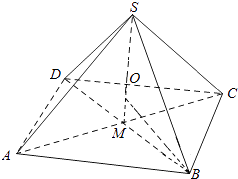
(ii)若O在在線段SM的延長線上,如圖二,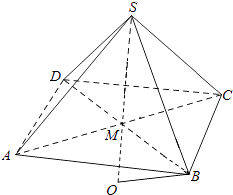
則OM=SO﹣SM=R﹣h,
∵SM⊥平面ABCD,
∴△OMB是直角三角形,
∴OM2+MB2=OB2 ,
∵OB=R,MB= ![]() BD=
BD= ![]() a,
a,
∴(h﹣R)2+ ![]() =R2 , 或(R﹣h)2+
=R2 , 或(R﹣h)2+ ![]() =R2
=R2
∴2hR=h2+ ![]() ,
,
即R= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() ≥3
≥3 ![]() =
= ![]() .
.
當且僅當 ![]() =
= ![]() 取等號,
取等號,
即h=3時R取得最小值 ![]() .
.
故選:A.
【考點精析】關于本題考查的棱錐的結構特征,需要了解側面、對角面都是三角形;平行于底面的截面與底面相似,其相似比等于頂點到截面距離與高的比的平方才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】設![]() 是正項數列
是正項數列![]() 的前
的前![]() 項和,且
項和,且![]() .
.
(Ⅰ)求數列![]() 通項公式;
通項公式;
(Ⅱ)是否存在等比數列![]() ,使
,使![]() 對一切正整數
對一切正整數![]() 都成立?并證明你的結論.
都成立?并證明你的結論.
(Ⅲ)設![]() (
(![]() ),且數列
),且數列![]() 的前
的前![]() 項和為
項和為![]() ,試比較
,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,已知下列條件解三角形:
①A=60°,a= ![]() ,b=1;
,b=1;
②A=30°,a=1,b=2;
③A=30°,c=10,a=6;
④A=30°,c=10,a=5,
其中有唯一解的序號為( )
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)為了監控某種零件的一條生產線的生產過程,檢驗員每天從該生產線上隨機抽取16個零件,并測量其尺寸(單位:cm).根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件的尺寸服從正態分布N(μ,σ2).
(1)假設生產狀態正常,記X表示一天內抽取的16個零件中其尺寸在(μ–3σ,μ+3σ)之外的零件數,求P(X≥1)及X的數學期望;
(2)一天內抽檢零件中,如果出現了尺寸在(μ–3σ,μ+3σ)之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
(ⅰ)試說明上述監控生產過程方法的合理性;
(ⅱ)下面是檢驗員在一天內抽取的16個零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經計算得![]() ,
,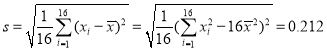 ,其中xi為抽取的第i個零件的尺寸,i=1,2,…,16.
,其中xi為抽取的第i個零件的尺寸,i=1,2,…,16.
用樣本平均數![]() 作為μ的估計值
作為μ的估計值![]() ,用樣本標準差s作為σ的估計值
,用樣本標準差s作為σ的估計值![]() ,利用估計值判斷是否需對當天的生產過程進行檢查?剔除
,利用估計值判斷是否需對當天的生產過程進行檢查?剔除![]() 之外的數據,用剩下的數據估計μ和σ(精確到0.01).
之外的數據,用剩下的數據估計μ和σ(精確到0.01).
附:若隨機變量Z服從正態分布N(μ,σ2),則P(μ–3σ<Z<μ+3σ)=0.997 4,0.997 416≈0.959 2,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)
在直角坐標系xOy中,曲線y=x2+mx–2與x軸交于A,B兩點,點C的坐標為(0,1).當m變化時,解答下列問題:
(1)能否出現AC⊥BC的情況?說明理由;
(2)證明過A,B,C三點的圓在y軸上截得的弦長為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
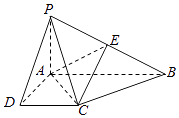
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 
(1)求證:平面PAD⊥平面PCD;
(2)試在棱PB上確定一點E,使截面AEC把該幾何體分成的兩部分PDCEA與EACB的體積比為2:1;
(3)在(2)的條件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定義域和值域均是[1,a],求實數a的值;
(2)若對任意的x1 , x2∈[1,a+1],總有|f(x1)﹣f(x2)|≤4,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com