Question

8．已知函數$y=\frac{1}{|2x|-1}$，求：
（1）函數的定義域，奇偶性并作出大致圖象；
（2）寫出函數的單調區間．

Answer 1

分析 （1）由|2x|-1≠0，可得x≠±$\frac{1}{2}$，即可求出函數的定義域，利用奇偶性的定義可得函數的奇偶性并作出大致圖象；
（2）根據圖象，即可寫出函數的單調區間．

解答 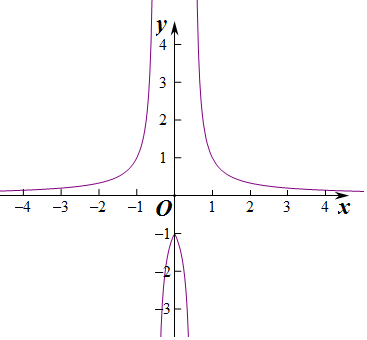解：（1）由|2x|-1≠0，可得x≠±$\frac{1}{2}$，
∴函數的定義域為{x|x≠±$\frac{1}{2}$}；
f（-x）=$\frac{1}{|-2x|-1}$=$\frac{1}{|2x|-1}$，
∴函數是偶函數；
圖象如圖所示；
（2）函數的單調遞增區間為
（-∞，-$\frac{1}{2}$），（-$\frac{1}{2}$，0）；單調遞減區間為（0，$\frac{1}{2}$），（$\frac{1}{2}$，+∞）．

點評 本題考查函數的定義域、奇偶性、單調性，考查函數圖象的作法，屬于中檔題．