Question

設y₁=a^3x+1，y₂=a^-2x（a＞0，a≠1），確定x為何值時，有：
（1）y₁=y₂ ；
（2）y₁＞y₂．

Answer 1

【答案】分析：先將兩個函數抽象為指數函數：y=a^x，則
（1）轉化為關于x的方程：3x-1=-2x求解．
（2）0＜a＜1，y=a^x是減函數，有3x-1＜-2x求解，當a＞1時，y=a^x是增函數，有3x-1＞-2x求解，然后兩種情況取并集．
解答：解：（1）因為y₁=y₂
∴3x+1=-2x
解之得：
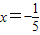
（2）因為a＞1，所以指數函數為增函數．
又因為y₁＞y₂，所以有3x-1＞-2x
解得；
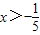
若0＜a＜1，指數函數為減函數．
因為y₁＞y₂，
所以有3x-1＜-2x
解得
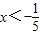
綜上：．
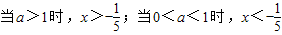
點評：本題主要考查指數不等式的解法，這類問題要轉化為指數函數的單調性來解．