
【題目】已知函數![]() 在區間
在區間![]() 上是單調函數.
上是單調函數.
(1)求實數![]() 的所有取值組成的集合
的所有取值組成的集合![]() ;
;
(2)試寫出![]() 在區間
在區間![]() 上的最大值
上的最大值![]() ;
;
(3)設![]() ,令
,令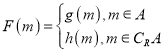 ,若對任意
,若對任意![]() ,總有
,總有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)因為![]() 為開口向上的二次函數,故其在對稱軸左邊單調遞減,對稱軸右邊單調遞增. 函數在區間
為開口向上的二次函數,故其在對稱軸左邊單調遞減,對稱軸右邊單調遞增. 函數在區間![]() 上是單調函數,等價于區間
上是單調函數,等價于區間![]() 在對稱軸的左邊或者右邊.列出不等式解出即可.
在對稱軸的左邊或者右邊.列出不等式解出即可.
(2)討論![]() 在
在![]() 上的單調性,分別求出其最大值,再寫成分段函數的形式即可.
上的單調性,分別求出其最大值,再寫成分段函數的形式即可.
(3)根據題意寫出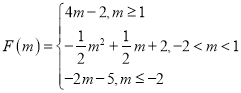 ,對任意
,對任意![]() ,總有
,總有![]() 等價于
等價于![]() 且
且![]() ,則分別討論
,則分別討論![]() 與
與 ![]() 的大小關系,找到其對應的
的大小關系,找到其對應的![]() 與
與![]() ,代入
,代入![]() 即可解出答案.
即可解出答案.
解:(1)對稱軸![]() .
.
所以![]() 或
或![]() .
.
(2)①當![]() ,即
,即![]() 時.
時.
函數![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() .
.
②當![]() ,即
,即![]() 時.
時.
函數![]() 在
在![]() 上單調遞減.
上單調遞減.
所以![]() .
.
綜上所述:![]() .
.
(3)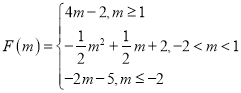 .
.
由題意得![]() ,
,![]() ,
,
畫出函數![]() 的圖像:
的圖像:
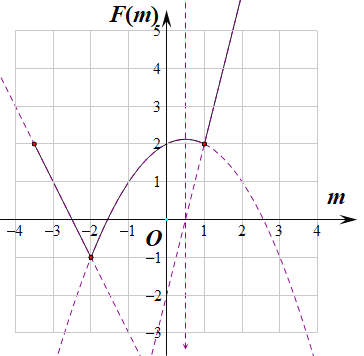
①當![]() 時,
時,![]() 在
在![]() 單調遞減.
單調遞減.
所以![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,舍.
,舍.
②當![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 上單調遞增.
上單調遞增. ![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
③當![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 上單調遞增.
上單調遞增. ![]() ,
, ![]() .
.
代入![]() ,化簡得
,化簡得![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() .
.
④當![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
⑤當![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,
,
綜上所述:![]() .即
.即![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在如圖的程序框圖中,若輸入![]() ,
,![]() ,則輸出的
,則輸出的![]() 值是( )
值是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/21/1907086498037760/1907898837975040/STEM/25d20caaa911497ea3baaf4f7dee45a3.png]
A. 3 B. 7 C. 11 D. 33
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,其中
是定義在R上的奇函數,其中![]() 為指數函數,且
為指數函數,且![]() 的圖象過定點
的圖象過定點![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若關于x的方程,![]() 有解,求實數a的取值范圍;
有解,求實數a的取值范圍;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,中美貿易摩擦不斷.特別是美國對我國華為的限制.盡管美國對華為極力封鎖,百般刁難,并不斷加大對各國的施壓,拉攏他們抵制華為5G,然而這并沒有讓華為卻步.華為在2018年不僅凈利潤創下記錄,海外增長同樣強勁.今年,我國華為某一企業為了進一步增加市場競爭力,計劃在2020年利用新技術生產某款新手機.通過市場分析,生產此款手機全年需投入固定成本250萬,每生產![]() (千部)手機,需另投入成本
(千部)手機,需另投入成本![]() 萬元,且
萬元,且  ,由市場調研知,每部手機售價0.7萬元,且全年內生產的手機當年能全部銷售完.
,由市場調研知,每部手機售價0.7萬元,且全年內生產的手機當年能全部銷售完.
(![]() )求出2020年的利潤
)求出2020年的利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千部)的函數關系式,(利潤=銷售額—成本);
(千部)的函數關系式,(利潤=銷售額—成本);
![]() 2020年產量為多少(千部)時,企業所獲利潤最大?最大利潤是多少?
2020年產量為多少(千部)時,企業所獲利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(1)求證:![]() ∥平面
∥平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 是菱形,
是菱形,![]() 交BD于點
交BD于點![]() ,
,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() 分別是
分別是![]() 的中點.
的中點.

(1)求證:EF//平面SAD;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農業合作社生產了一種綠色蔬菜共![]() 噸,如果在市場上直接銷售,每噸可獲利
噸,如果在市場上直接銷售,每噸可獲利![]() 萬元;如果進行精加工后銷售,每噸可獲利
萬元;如果進行精加工后銷售,每噸可獲利![]() 萬元,但需另外支付一定的加工費,總的加工
萬元,但需另外支付一定的加工費,總的加工![]() (萬元)與精加工的蔬菜量
(萬元)與精加工的蔬菜量![]() (噸)有如下關系:
(噸)有如下關系: 設該農業合作社將
設該農業合作社將![]() (噸)蔬菜進行精加工后銷售,其余在市場上直接銷售,所得總利潤(扣除加工費)為
(噸)蔬菜進行精加工后銷售,其余在市場上直接銷售,所得總利潤(扣除加工費)為![]() (萬元).
(萬元).
(1)寫出![]() 關于
關于![]() 的函數表達式;
的函數表達式;
(2)當精加工蔬菜多少噸時,總利潤最大,并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com