Question

【題目】在正項數列{an}中，已知a1=1，且滿足an+1=2an （n∈N*）
（Ⅰ）求a2 ， a3；
（Ⅱ）證明．an≥ ．

Answer 1

【答案】解：（Ⅰ）∵在正項數列{an}中，a1=1，且滿足an+1=2an （n∈N*），

∴ = ，

= ．

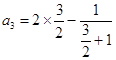證明：（Ⅱ）①當n=1時，由已知 ，成立；

②假設當n=k時，不等式成立，即 ，

∵f（x）=2x﹣ 在（0，+∞）上是增函數，

∴ ≥

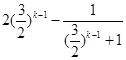
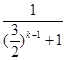
=（ ）k+ （ ）k﹣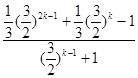

=（ ）k+

=（ ）k+ ，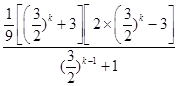

∵k≥1，∴2×（ ）k﹣3 ﹣3=0，

∴ ，

即當n=k+1時，不等式也成立．

根據①②知不等式對任何n∈N*都成立

【解析】（Ⅰ）利用遞推公式能依次求出a2，a3．（Ⅱ）利用數數歸納法證明：先驗證當n=1時， ，成立，再假設當n=k時， ，由f（x）=2x﹣ 在（0，+∞）上是增函數，推導出 ，由此能證明an≥ ．
【考點精析】解答此題的關鍵在于理解數列的通項公式的相關知識，掌握如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式．