A
分析:設(shè)M(x)=|t+x|+|t-x|,由于M(-x)=M(x),故它是偶函數(shù),畫出其圖象如圖所示,結(jié)合圖象得當(dāng)0<|x|<1,0<|t|≤1時(shí),|t+x|+|t-x|<2;又設(shè)N(x)=|f(tx+1)|,由于N(-x)=N(x),故它也是偶函數(shù),當(dāng)0<t≤1,0<x<1時(shí),N(x)=tx+
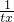
利用基本不等式得出N(x)有最小值2.從而得出答案.
解答:
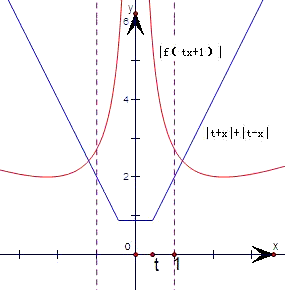
解:設(shè)M(x)=|t+x|+|t-x|,由于M(-x)=M(x),
故它是偶函數(shù),
其圖象如圖所示,它在[-1,1]上的最大值為2,
故當(dāng)0<|x|<1,0<|t|≤1時(shí),|t+x|+|t-x|<2;
又設(shè)N(x)=|f(tx+1)|=|tx+
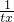
|,
由于N(-x)=N(x),故它也是偶函數(shù),
當(dāng)0<t≤1,0<x<1時(shí),N(x)=tx+
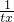
≥2,
故當(dāng)0<|x|<1,0<|t|≤1時(shí),N(x)=|f(tx+1)|≥2,
所以,當(dāng)0<|x|<1,0<|t|≤1時(shí),|t+x|+|t-x|<|f(tx+1)|.
故選A.
點(diǎn)評(píng):本小題主要考查函數(shù)單調(diào)性的應(yīng)用、函數(shù)奇偶性的應(yīng)用、不等式的解法等基礎(chǔ)知識(shí),考查運(yùn)算求解能力,考查數(shù)形結(jié)合思想、化歸與轉(zhuǎn)化思想.屬于基礎(chǔ)題.

 -1,當(dāng)0<|x|<1,0<|t|≤1時(shí),|t+x|+|t-x|與|f(tx+1)|的大小關(guān)系是
-1,當(dāng)0<|x|<1,0<|t|≤1時(shí),|t+x|+|t-x|與|f(tx+1)|的大小關(guān)系是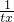 利用基本不等式得出N(x)有最小值2.從而得出答案.
利用基本不等式得出N(x)有最小值2.從而得出答案. 解:設(shè)M(x)=|t+x|+|t-x|,由于M(-x)=M(x),
解:設(shè)M(x)=|t+x|+|t-x|,由于M(-x)=M(x),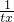 |,
|,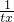 ≥2,
≥2,


 已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<