
(本小題14分)四棱錐![]() 中,底面
中,底面![]() 為矩形,側(cè)面
為矩形,側(cè)面![]() 底面
底面![]() ,
,![]()
![]() .
.
(I)取![]() 的中點為
的中點為![]() ,
,![]() 的中點為
的中點為![]() ,證明:FG∥面
,證明:FG∥面![]() ;
;
 (II)證明:
(II)證明:![]() .
.
解答
(I)證明:取AB中點H,連接GH,CH
因為G是AE中點,所以HG∥=![]() BE,又因為矩形BCDE,所以BE∥=CD,且F是CD中點,
BE,又因為矩形BCDE,所以BE∥=CD,且F是CD中點,
所以HG∥=CF,所以四邊形FGHC是平行四邊形,所以FG∥CH,………………………………4分
又因為FG![]() 平面ABC,CH
平面ABC,CH![]() 平面ABC,所以FG∥面
平面ABC,所以FG∥面![]() ;………………………………7分
;………………………………7分
(II)取BC中點Q,連接AQ,DQ
因為AC=AB,所以AQ⊥BC,
因為側(cè)面![]() 底面
底面![]() ,AQ
,AQ![]() 平面ABC,平面ABC∩平面
平面ABC,平面ABC∩平面![]() =BC,
=BC,
所以AQ⊥平面BCDE,……………………………………………………………………………………8分
因為CE![]() 平面BCD ,所以 CE⊥AQ……………………………………………………………9分
平面BCD ,所以 CE⊥AQ……………………………………………………………9分
又在矩形BCDE中,![]() ,BE=
,BE=![]() ,CQ=1, 所以
,CQ=1, 所以![]()
所以Rt△CDQ∽Rt△BCE,所以∠DQC=∠CEB, ………………………………………………10分
所以∠DQC+∠BCE=∠CEB+∠BCE=90o ,所以CE⊥BQ…………………………12分(其他方法參照給分)
因為AQ∩BQ=Q,所以CE⊥平面ADQ,………………………………………………13分
AD![]() 平面ADQ,所以
平面ADQ,所以![]() ………………………………………………………………14分
………………………………………………………………14分


科目:高中數(shù)學(xué) 來源: 題型:
(本小題共14分)
如圖,四棱錐![]() 的底面是正方形,
的底面是正方形,![]() ,點E在棱PB上。
,點E在棱PB上。

(Ⅰ)求證:平面![]() ;
;
(Ⅱ)當(dāng)![]() 且E為PB的中點時,求AE與平面PDB所成的角的大小。
且E為PB的中點時,求AE與平面PDB所成的角的大小。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣東省肇慶市高三數(shù)學(xué)復(fù)習(xí)必修2立體幾何部分試卷 題型:解答題
(本小題14分)已知四棱錐P-ABCD,底面ABCD是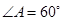 、邊長為
、邊長為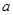 的菱形,又
的菱形,又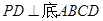 ,且PD=CD,點M、N分別是棱AD、PC的中點.
,且PD=CD,點M、N分別是棱AD、PC的中點.

(1)證明:DN//平面PMB;
(2)證明:平面PMB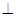 平面PAD;
平面PAD;
(3)求點A到平面PMB的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆廣東省高二上學(xué)期期末考試理科數(shù)學(xué)試卷 題型:解答題
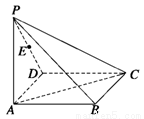
(本小題14分)如圖所示,在四棱錐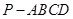 中,底面
中,底面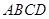 為矩形,側(cè)棱
為矩形,側(cè)棱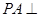 底面
底面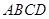 ,
, 為
為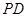 的中點.
的中點.
(1)求直線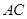 與
與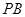 所成角的余弦值;
所成角的余弦值;
(2)在側(cè)面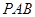 內(nèi)找一點
內(nèi)找一點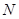 ,使
,使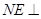 平面
平面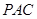 ,并分別求出點
,并分別求出點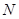 到
到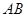 和
和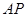 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:北京市西城區(qū)2010年高三一模數(shù)學(xué)(理)試題 題型:解答題
(本小題滿分14分)
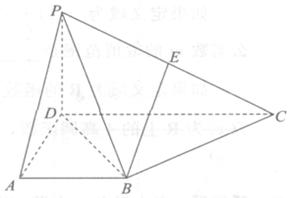
在四棱錐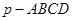 中,側(cè)面
中,側(cè)面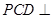 底面
底面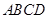 ,
,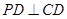 ,
,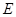 為
為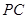 中點,底面
中點,底面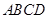 是直角梯形,
是直角梯形,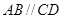 ,
,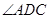 =90°,
=90°,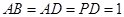 ,
,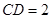 。
。
(I)求證: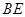
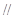 平面
平面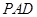 ;
;
(II)求證: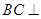 平面
平面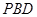 ;
;
(III)設(shè)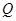 為側(cè)棱
為側(cè)棱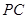 上一點,
上一點,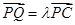 ,試確定
,試確定 的值,使得二面角
的值,使得二面角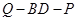 為45°。
為45°。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年廣東省高考沖刺強化訓(xùn)練試卷三文科數(shù)學(xué) 題型:解答題
(本小題滿分14分)如圖,在四棱錐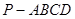 中,底面ABCD是正方形,側(cè)棱
中,底面ABCD是正方形,側(cè)棱 底面ABCD,
底面ABCD, ,E是PC的中點,作
,E是PC的中點,作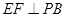 交PB于點F.
交PB于點F.
(I) 證明: PA∥平面EDB;
(II) 證明:PB⊥平面EFD;
(III) 求三棱錐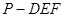 的體積.
的體積.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com