
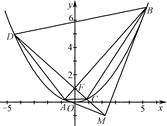
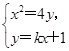 消去y,得x2-4kx-4=0,顯然Δ=16k2+16>0.
消去y,得x2-4kx-4=0,顯然Δ=16k2+16>0.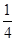 x2,所以y′=
x2,所以y′=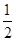 x,所以,直線AM的斜率為kAM=
x,所以,直線AM的斜率為kAM=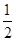 x1,
x1,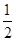 x1(x-x1),又
x1(x-x1),又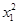 =4y1,
=4y1,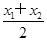 ,即A、M、B三點的橫坐標成等差數列.
,即A、M、B三點的橫坐標成等差數列.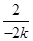 =-
=-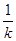 ,則直線MF的方程為y=-
,則直線MF的方程為y=-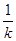 x+1,
x+1,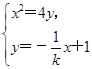 消去y,得x2+
消去y,得x2+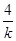 x-4=0,顯然Δ=
x-4=0,顯然Δ=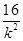 +16>0,
+16>0,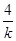 ,x3x4=-4,又|AB|=
,x3x4=-4,又|AB|=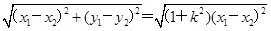
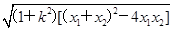 =4(k2+1),
=4(k2+1),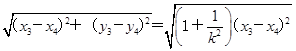 =
=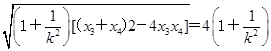 ,
,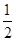 |AB|·|CD|=8
|AB|·|CD|=8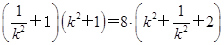 ≥32,
≥32,

科目:高中數學 來源:不詳 題型:解答題
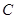 上任意一點
上任意一點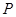 作直線
作直線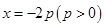 的垂線,垂足為
的垂線,垂足為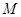 ,且
,且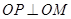 .
.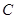 的方程;
的方程;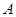 、
、 是曲線
是曲線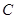 上兩個不同點,直線
上兩個不同點,直線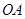 和
和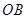 的傾斜角分別為
的傾斜角分別為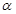 和
和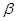 ,
,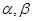 變化且
變化且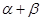 為定值
為定值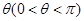 時,證明直線
時,證明直線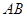 恒過定點,
恒過定點,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com