解:(Ⅰ)函數f(x)=ln|x|-x
2+ax的定義域為{x|x∈R,x≠0}.
當x>0時,f(x)=lnx-x
2+ax,∴
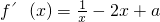
; …(1分)
當x<0時,f(x)=ln(-x)-x
2+ax,∴
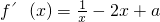
; …(3分)
綜上可得
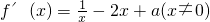
.…(4分)
(Ⅱ)∵
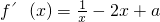
=
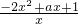
,x
1、x
2為函數f(x)的兩個極值點,
∴x
1、x
2為方程-2x
2+ax+1=0的兩根,所以
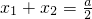
,
又∵
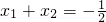
,∴a=-1.…(5分)
此時,
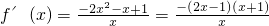
,
由f'(x)≥0得
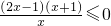
,
當x>0時,
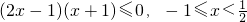
,此時
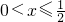
;
當x<0時,(2x-1)(x+1)≥0,∴x≤-1或x≥

,此時x≤-1.
∴當f'(x)≥0時,x≤-1或
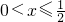
.…(7分)
當f'(x)≤0時,同理解得
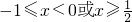
.…(8分)
綜上可知a=-1滿足題意,且函數f(x)的單調遞增區間為(-∞,-1]和
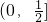
.…(9分)
(Ⅲ)∵
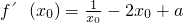
,又
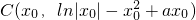
,
∴切線l的方程為
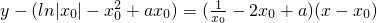
,
即
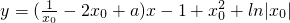
(x
0為常數).…(10分)
令
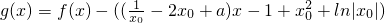
=
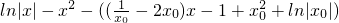
,
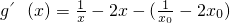
=
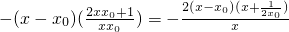
,(11分)
當x
0>0時,x、g'(x)、g(x)的關系如下表:
| x | 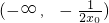 | 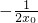 | 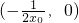 | (0,x0) | x0 | (x0,+∞) |
| g'(x) | + | 0 | - | + | 0 | - |
| g(x) | ↗ | 極大值 | ↘ | ↗ | 極大值 | ↘ |
當x
0<0時,x、g'(x)、g(x)的關系如下表:
| x | (-∞,x0) | x0 | (x0,0) | 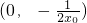 | 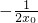 | 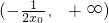 |
| g'(x) | + | 0 | - | + | 0 | - |
| g(x) | ↗ | 極大值 | ↘ | ↗ | 極大值 | ↘ |
函數f(x)=ln|x|-x
2+ax的圖象恒在直線l的下方或直線l上,
等價于g(x)≤0對x≠0恒成立.
∴只需g(x
0)≤0和
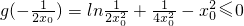
同時成立.…(12分)
∵g(x
0)=0,∴只需
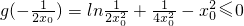
.
下面研究函數
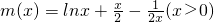
,
∵
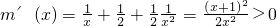
,
∴m(x)在(0,+∞)上單調遞增,
注意到m(1)=0,∴當且僅當0<x≤1時,m(x)≤0.…(13分)
∴當且僅當
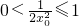
時,
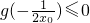
,
由
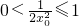
解得
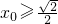
或
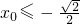
.
∴x
0的取值范圍是
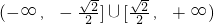
.…(14分)
分析:(Ⅰ)確定函數的定義域,分類討論,將函數化簡,再求導函數即可;
(Ⅱ)根據x
1、x
2為函數f(x)的兩個極值點,利用韋達定理,可求a的值,即得到函數解析式,求導函數,利用f'(x)≥0,可得函數f(x)的單調遞增區間;
(Ⅲ)確定切線l的方程,再構造新函數g(x),求導數,確定函數的單調性與極值,從而函數f(x)=ln|x|-x
2+ax的圖象恒在直線l的下方或直線l上,等價于g(x)≤0對x≠0恒成立,即只需g(x
0)≤0和
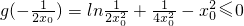
,由此可得x
0的取值范圍.
點評:本題主要考查函數、導數等基礎知識,考查推理論證能力、運算求解能力,考查數形結合思想、化歸與轉化思想、分類與整合思想、函數與方程思想.

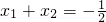 ,試求函數f(x)的單調遞增區間;
,試求函數f(x)的單調遞增區間;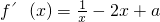 ; …(1分)
; …(1分)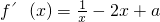 ; …(3分)
; …(3分)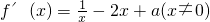 .…(4分)
.…(4分)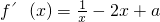 =
=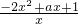 ,x1、x2為函數f(x)的兩個極值點,
,x1、x2為函數f(x)的兩個極值點,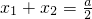 ,
,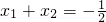 ,∴a=-1.…(5分)
,∴a=-1.…(5分)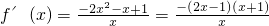 ,
,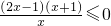 ,
,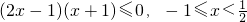 ,此時
,此時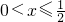 ;
; ,此時x≤-1.
,此時x≤-1.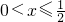 .…(7分)
.…(7分)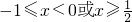 .…(8分)
.…(8分)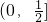 .…(9分)
.…(9分)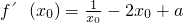 ,又
,又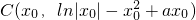 ,
,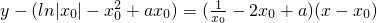 ,
,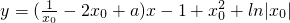 (x0為常數).…(10分)
(x0為常數).…(10分)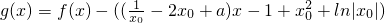 =
=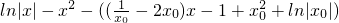 ,
,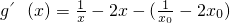 =
=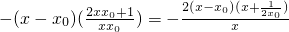 ,(11分)
,(11分)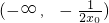
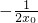
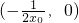
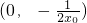
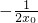
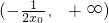
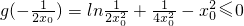 同時成立.…(12分)
同時成立.…(12分)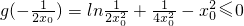 .
.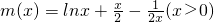 ,
,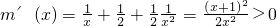 ,
,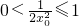 時,
時,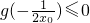 ,
,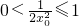 解得
解得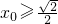 或
或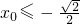 .
.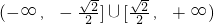 .…(14分)
.…(14分)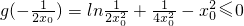 ,由此可得x0的取值范圍.
,由此可得x0的取值范圍.

 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案